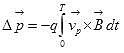A distanza di 150 anni dalla pubblicazione del lavoro di Maxwell in cui compaiono le famose equazioni che reggono tutto l’elettromagnetismo e identificano la luce come onda elettromagnetica, l’autore riesamina la loro importanza e le loro conseguenze nello sviluppo della scienza. L’importanza teorica risiede nell’unificazione dei fenomeni elettrici e magnetici, quasi una profezia del tentativo di unificazione delle forze fondamentali, che da quasi un secolo è uno degli obiettivi, solo parzialmente riuscito, della Fisica. Ma anche nel collegamento con la nascita della relatività attraverso le trasformazioni di Lorentz. Infine anche i limiti di queste equazioni a livello dei fenomeni atomici hanno avuto conseguenze importanti, ma non hanno intaccato la loro validità nell’ambito dei fenomeni macroscopici.
Scheda di Approfondimento n°1
Le Equazioni di Maxwell
Anche se completamente equivalenti, le trascrizioni delle equazioni di Maxwell possono essere diverse tra loro e da quella originariamente usata da Maxwell.
Indicando con![]() ,
, ![]() ,
, ![]() , e
, e ![]() , rispettivamente, i vettori Campo e Induzione Elettrica, Campo e Induzione Magnetica, le equazioni di Maxwell in forma differenziale, possono essere scritte nella forma seguente:
, rispettivamente, i vettori Campo e Induzione Elettrica, Campo e Induzione Magnetica, le equazioni di Maxwell in forma differenziale, possono essere scritte nella forma seguente:
 dove div e rot sono combinazioni di derivate parziali del primo ordine rispetto a x, y e z, note rispettivamente come operatore divergenza e operatore rotore mentre
dove div e rot sono combinazioni di derivate parziali del primo ordine rispetto a x, y e z, note rispettivamente come operatore divergenza e operatore rotore mentre ![]() , la densità volumica di carica, e
, la densità volumica di carica, e ![]() , il vettore densità di corrente, sono le sorgenti del campo (a creare i campi sono infatti cariche e correnti).
, il vettore densità di corrente, sono le sorgenti del campo (a creare i campi sono infatti cariche e correnti).
I vettori ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() sono legati fra di loro dalle funzioni:
sono legati fra di loro dalle funzioni:
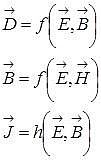 che esprimono le proprietà elettriche e magnetiche del mezzo in cui i campi viaggiano.
che esprimono le proprietà elettriche e magnetiche del mezzo in cui i campi viaggiano.
Per campi deboli, escludendo la presenza nel mezzo di materiali ferroelettrici e/o ferromagnetici, f, g ed h si riducono a semplici relazioni lineari tra le componenti di coppie dei vettori stessi:
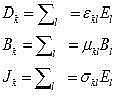 Le proprietà del mezzo sono ora espresse dalle componenti
Le proprietà del mezzo sono ora espresse dalle componenti ![]() di tre grandezze tensoriali: permeabilità o tensore dielettrico
di tre grandezze tensoriali: permeabilità o tensore dielettrico ![]() , permeabilità o tensore magnetico µ e conducibilità
, permeabilità o tensore magnetico µ e conducibilità ![]() . In generale
. In generale ![]() ,
, ![]() ,
, ![]() e
e ![]() non sono paralleli.
non sono paralleli.
Nel caso di un mezzo omogeneo ed isotropo, in particolare nel vuoto, ![]() diventa parallelo a
diventa parallelo a ![]() , e
, e ![]() ad
ad ![]() e i tensori si riducono ai noti scalari costante dielettrica,
e i tensori si riducono ai noti scalari costante dielettrica, ![]() , permeabilità magnetica,
, permeabilità magnetica, ![]() e conducibilità
e conducibilità ![]() .
.
Osserviamo che:
La soluzione delle equazioni è sempre possibile, (in modi che qui non andremo ad affrontare) quando siano note la distribuzione delle cariche e delle correnti che creano i campi e le proprietà elettriche e magnetiche del mezzo.
Le equazioni di Maxwell sono lineari pertanto vale il principio di sovrapposizione. Questa proprietà, combinata con i teoremi di Fourier consente di studiare le equazioni di Maxwell assumendo che
 e
e  siano funzioni armoniche: in questo caso le equazioni possono essere trattate più facilmente.
siano funzioni armoniche: in questo caso le equazioni possono essere trattate più facilmente.Semplici manipolazioni delle equazioni danno:

equazione di continuità che mostra che le equazioni di Maxwell soddisfano la conservazione delle carica.La forza di Lorentz:

(x indica il prodotto vettore) estraibile anch’essa dalle equazioni di Maxwell permette di studiare il comportamento di una o più cariche immerse in un campo elettromagnetico(*)
(*) Allo studio e risoluzione delle equazioni di Maxwell hanno dato un grande contributo anche due fisici quasi omonimi Ludvig Valentin Lorenz (1829-1891), danese, e Hendrik Antoon Lorentz (1853-1928), olandese. A causa di questa quasi omonimia non è chiaro a chi spetti la primogenitura nel ricavare questa forza. Di certo entrambi hanno dato contributi che portano a tale relazione: L.V. Lorenz, scrivendo per primo gli integrali che forniscono i potenziali ritardati utilizzati per risolvere le equazioni di Maxwell; H.A. Lorentz, individuando le trasformazioni dette appunto di Lorentz sotto le quali le equazioni di Maxwell risultano invarianti.
Scheda di Approfondimento n° 2
Proprietà delle Onde Elettromagnetiche
Applicando in maniera opportuna gli operatori div e rot alle equazioni di Maxwell, ponendosi a grande distanza dalle sorgenti dei campi si arriva a:
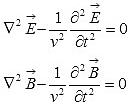 (
(![]() 2 è una combinazione di derivate parziali di secondo grado nota come Laplaciano), dove ha le dimensioni di una velocità ed è il risultato delle proprietà del mezzo.
2 è una combinazione di derivate parziali di secondo grado nota come Laplaciano), dove ha le dimensioni di una velocità ed è il risultato delle proprietà del mezzo.
In un mezzo omogeneo e isotropo:
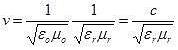 Nel vuoto (εr = 1 e μr = 1):
Nel vuoto (εr = 1 e μr = 1):
Pertanto:
 e
e  sono le due componenti di un unico campo, il campo elettromagnetico che si propaga anche nel vuoto;
sono le due componenti di un unico campo, il campo elettromagnetico che si propaga anche nel vuoto;La velocità di propagazione coincide con la velocità della luce nello stesso mezzo;
Se il mezzo è omogeneo l’indice di rifrazione di un mezzo è dato da:

è l’indice di rifrazione del mezzo (se le proprietà elettromagnetiche del mezzo e quindi εr dipendono dalla frequenza anche n dipende dalla frequenza);
A grande distanza dalle sorgenti del campo (approssimazione delle onde piane) l’onda
 e l’onda
e l’onda  sono entrambi trasversali, mutuamente ortogonali e viaggiano in fase. Pertanto le onde elettromagnetiche possono essere polarizzate;
sono entrambi trasversali, mutuamente ortogonali e viaggiano in fase. Pertanto le onde elettromagnetiche possono essere polarizzate;L’onda elettromagnetica trasporta energia equiripartita tra il campo
 e il campo
e il campo  ; ogni modifica di
; ogni modifica di si ripercuote su
si ripercuote su  e viceversa in modo da mantenere l’equipartizione dell’energia (non possono quindi esistere onde solo elettriche o solo magnetiche). Il flusso di energia è dato dal Vettore di Poynting:
e viceversa in modo da mantenere l’equipartizione dell’energia (non possono quindi esistere onde solo elettriche o solo magnetiche). Il flusso di energia è dato dal Vettore di Poynting: 
Nell’attraversare un mezzo in cui sono presenti cariche in grado di sentire la forza di Lorentz in un periodo T l’onda cede a una carica una energia:
ΔԐ = e le trasmette un impulso:
e le trasmette un impulso: 
Pertanto colpendo una superficie assorbente l’onda esercita una pressione:

Con a = 1 se la radiazione incide normalmente alla superficie o a = 1/3 se le direzioni d’arrivo della radiazione sono distribuite isotropicamente. Se la superficie è riflettente i precedenti valori di a vanno raddoppiati.
Una carica q che risente una accelerazione
 perde energia sotto forma di onde elettromagnetiche. Se la velocità v è piccola rispetto alla velocità della luce c la potenza irraggiata è data dalla relazione:
perde energia sotto forma di onde elettromagnetiche. Se la velocità v è piccola rispetto alla velocità della luce c la potenza irraggiata è data dalla relazione:
![]()
Giorgio Sironi
(Università degli Studi di Milano-Bicocca)
© Pubblicato sul n° 53 di Emmeciquadro

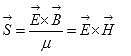
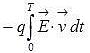 e le trasmette un impulso:
e le trasmette un impulso: