Che cosa significa oggi per un insegnante conoscere i contenuti della propria disciplina? Rispondere a questa domanda è di capitale importanza per ogni docente che non voglia cedere alla tentazione di semplificazioni manualistiche che riducono la competenza all’applicazione meccanica di schemi e regole. L’autore, ripercorrendo la storia della fisica, traccia un itinerario concettuale che, evidenziandone le tappe salienti, fornisce criteri di selezione utili per una programmazione criticamente fondata.
Si può ritenere che la Fisica nel senso moderno del termine sia nata nel Rinascimento. Fin dal XVI-XVII secolo si è stabilito un nuovo metodo (soprattutto per mezzo del lavoro pionieristico di Galileo) basato su un continuo feed-back fra idee teoriche ed esperimenti con largo uso del linguaggio matematico. A parte questioni di enfasi, tale metodo è rimasto sostanzialmente inalterato fino ai nostri giorni. In conseguenza di esso, tuttavia, si sono progressivamente verificati non solo un grande incremento delle nostre conoscenze sulla Natura, ma anche diversi e importanti drastici cambiamenti nella concettualizzazione dei fenomeni. Talvolta questi cambiamenti sembrano contraddire così pesantemente gli schemi precedenti da porre seri interrogativi sul valore conoscitivo di una scienza che sembra essere in ogni momento in uno stato provvisorio, eppure pretende di aver raggiunto risultati permanenti, in molti casi anche risultati definitivi.
In questo articolo voglio riflettere su tali problemi e suggerire che le idee di modello e di conoscenza analogica possano aiutare a comprendere meglio la situazione.
Breve prospettiva sullo sviluppo di alcuni modelli concettuali
Il primo capitolo della Fisica che ha acquistato la forma di una teoria organica è stata ovviamente la Meccanica. Ciò è dovuto soprattutto al lavoro di Newton e di molti altri scienziati del XVIII e del XIX secolo.
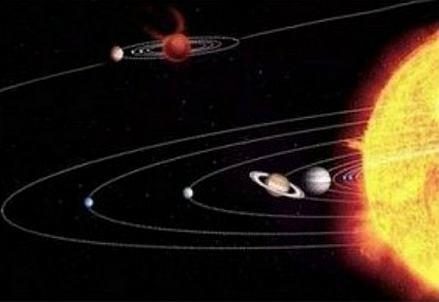
L’idea centrale della Meccanica è quella di «punto materiale». In una certa classe di fenomeni possiamo ignorare la forma e le dimensioni di un corpo. Possiamo identificarlo semplicemente con la sua massa e la sua posizione, e scrivere un sistema di equazioni che stabilisce come le sue coordinate variano nel tempo. Questa idealizzazione è già sufficiente per la trattazione del moto dei gravi in prossimità del suolo e del moto di rivoluzione dei pianeti intorno al sole. Anche il comportamento dei corpi estesi può poi essere facilmente compreso considerandoli come un aggregato di piccole parti, trattate come singoli punti materiali. In questo modo è stato possibile costruire una teoria del corpo rigido, una fluidodinamica e in seguito una teoria dell’elasticità.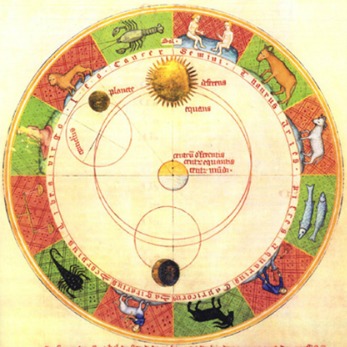 
La perfezione formale raggiunta dalla Meccanica e i suoi successi divennero tali che in breve molti scienziati si convinsero che tutti gli altri fenomeni fisici avrebbero potuto essere compresi all’interno del suo schema. [Immagine a sinistra: Rappresentazione del sistema planetario secondo il modello Tolemaico]
Newton stesso credeva che ciò che mancava a questo programma fosse solo una ragionevole teoria della struttura microscopica della materia: dopo di che sarebbe dovuto diventare possibile ridurre tutte le forze (incluse quelle elettriche e magnetiche) alla sola forza gravitazionale.
È anche ben nota la famosa affermazione di Laplace secondo la quale un’intelligenza sufficientemente potente avrebbe dovuto essere, in linea di principio, capace di ricostruire l’intera storia passata e futura dell’universo dalla conoscenza delle posizioni e delle velocità a un determinato istante di tutte le particelle che lo costituiscono.
I primi dubbi sulla possibilità di comprendere la Natura esclusivamente in termini meccanici sorsero, nella prima metà del XIX secolo, come conseguenza dell’idea di campo introdotta da Ampère e Faraday. Come è ben noto, ogni tentativo di interpretazione meccanica del campo elettromagnetico è stata definitivamente abbandonata all’inizio del XX secolo dopo la formulazione della teoria di Maxwell e la comparsa della Teoria della Relatività. Ci si è resi conto che il campo deve essere considerato come un’entità completamente nuova. Benché priva di ogni supporto «materiale», questa nuova entità è in un certo senso molto concreta: può essere percepita direttamente in certe condizioni, può essere misurata, è in grado di trasportare energia e quantità di moto. In particolare il nuovo concetto di campo permette di risolvere il paradosso newtoniano dell’azione a distanza, che è diventato in contraddizione con le regole della relatività.
Il mutamento nell’attegiamento mentale è stato drastico. Si è dovuto semplicemente rinunciare alla speranza di riuscire a comprendere ogni cosa esclusivamente in termini di relazioni spaziotemporali fra gli oggetti.
Un nuovo anche più importante cambiamento si è verificato con il sorgere della Fisica Quantistica. Ci si rese conto che la Meccanica Classica non solo risultava insufficiente nella trattazione dei fenomeni elettromagnetici, ma era anche assolutamente inadeguata a trattare gli stessi componenti elementari della materia, ai quali in passato si era creduto potesse applicarsi nel modo più appropriato. Infatti l’idea di punto materiale, sulla quale era basata l’intera Meccanica Classica, doveva essere drasticamente modificata e perdeva gran parte del suo significato originale.
L’idea fondamentale della nuova teoria era che a ognuno degli oggetti che noi chiamiamo particelle fosse associato un campo che doveva soddisfare a un’appropriata equazione del tipo di quella delle onde.
Nella formulazione più elementare della teoria dei quanti, la cosiddetta Meccanica Quantistica di «prima quantizzazione», il quadrato del valore assoluto dell’intensità del campo è correlato, come è noto, alla probabilità di «localizzare» in una determinata posizione la particella per mezzo di un adeguato apparato sperimentale. In questo senso il campo e l’equazione delle onde possono essere considerati come semplici strumenti matematici per ottenere previsioni osservabili. 
Tuttavia, con le onde associate alle particelle è possibile ripetere esperimenti di interferenza e diffrazione del tutto analoghi a quelli eseguiti con la luce. [Immagine che segue a sinistra: figura di diffrazione di elettroni ottenuta con monocristallo d’oro]
Con un fascio di elettroni è possibile ottenere fenomeni di diffrazione sui cristalli simili a quelli ottenuti con i raggi X, ed è anche possibile riprodurre l’esperienza delle due fenditure di Young. [Immagine a destra: figura di diffrazione di raggi X ottenuta con lo stesso monocristallo d’oro]
In tale contesto, è importante sottolineare che in un dispositivo sperimentale in cui le particelle sono contate singolarmente, la distribuzione delle frange di interferenza è progressivamente ricostruita come conseguenza della distribuzione statistica delle particelle sullo schermo.
È chiaro che il concetto stesso di interferenza è in contraddizione con l’idea di una particella puntiforme che segue una traiettoria continua. Se nell’esperienza di Young ci limitiamo anche solo a pensare che una particella viaggi attraverso una ben definita fenditura, siamo costretti inevitabilmente a concludere che l’interferenza è impossibile.
Nella Fisica Quantistica il solo senso in cui l’idea di un punto materiale ancora rimane è quello collegato al fatto che in ogni istante la particella rimane un oggetto individuale che, di volta in volta, può agire solo su uno di un insieme di rivelatori arbitrariamente piccoli. Come è ben noto, il principio di indeterminazione di Heisenberg stabilisce i limiti entro i quali gli effetti quantistici sono trascurabili e la rappresentazione classica può essere applicata.
Il drastico distacco dalle idee classiche diviene ancora più evidente quando si considera la Teoria Quantistica dei Campi (seconda quantizzazione) piuttosto che la Meccanica Quantistica. Come è noto quest’ultimo sviluppo è essenziale per rendere compatibile la quantizzazione con la Relatività. Nella Teoria Quantistica dei Campi le particelle sono considerate come «quanti» di appropriati campi. Così esse diventano solo un’espressione del fatto che l’energia e la quantità di moto possono cambiare solo per quantità discrete. Parlare di un elettrone, due elettroni, molti elettroni significa soltanto specificare lo stato di un particolare campo. In tal modo la particella perde anche l’individualità che ancora conservava nella prima quantizzazione. In un dato processo alcune particelle possono scomparire e altre particelle essere create; questo fatto è semplicemente una manifestazione degli scambi di energia e quantità di moto fra differenti campi.
Il problema del valore conoscitivo della Fisica
La descrizione dello sviluppo delle idee in Fisica che ho tentato, allo scopo di mostrare il progressivo crollo delle precedenti idee teoriche basilari, e la necessità di sostituirle con altre sempre nuove, porta naturalmente a sollevare il problema del significato e del valore della conoscenza che abbiamo ottenuto fino ad ora. Per prima cosa dovrebbe essere ovvio che è impossibile mantenere come valide le opinioni di alcuni scienziati, in particolare del XVIII e XIX secolo, secondo i quali la Fisica poteva fornire una comprensione esaustiva e in qualche modo definitiva della realtà. La storia ci insegna che, come la ricerca procede, tutte le teorie mostrano i loro limiti e nuove teorie devono essere costruite. 
In molti casi le nuove teorie si sviluppano nell’ambito dello stesso ordine di idee delle vecchie, che sono inglobate in esse e rimangono valide in situazioni più particolari. [Immagine a destra: Max Planck (1858-1947)]
Altre volte, come abbiamo sottolineato, gli stessi strumenti concettuali devono essere radicalmente modificati. In particolare, nel trattare con scale estremamente piccole, dobbiamo liberarci in gran parte della nostra visione intuitiva e costruire teorie in cui la Matematica acquista il ruolo di uno strumento linguistico insostituibile invece di essere semplicemente un mezzo di calcolo. È chiaro inoltre che il progresso in Fisica non consiste mai in un aumento puramente quantitativo della nostra conoscenza e che a ogni stadio i nostri risultati devono essere considerati parziali e provvisori.
Di fronte alla situazione sopra delineata e alla difficoltà di interpretazione della Teoria dei Quanti molti scienziati e filosofi della scienza hanno adottato un atteggiamento puramente pragmatico e strumentale. Questo atteggiamento consiste nel considerare la teoria come una semplice registrazione di regolarità e correlazioni fra fenomeni, con lo scopo di fare previsioni nel modo più economico, ma senza alcun rapporto con una realtà oggettiva.
Negli anni Venti e Trenta del XX secolo il punto di vista strumentalista è stato interpretato nel modo più esplicito dal movimento neopositivista e per qualche tempo questa filosofia ha preteso di essere considerata la filosofia ufficiale della Fisica.
Tuttavia questa posizione radicale è insostenibile ed è per di più in contraddizione con la motivazione principale della stessa ricerca scientifica.
In primo luogo, la nozione di una realtà oggettiva deriva dalla esperienza assolutamente basilare che non possiamo modificare «il mondo» a nostro piacimento e che dobbiamo «comprenderlo », per poter agire su di esso. Io ritengo che nessuno possa pensare seriamente di poter eliminare un concetto di realtà.
In secondo luogo, da un punto di vista puramente convenzionalista o strumentalista, non c’è posto per quell’elemento teorico che è così essenziale in Fisica e così profondamente correlato a parole come «comprensione» o «spiegazione». In quella prospettiva una teoria si dovrebbe ridurre a un insieme di tautologie, o a un semplice criterio di ordinamento dei diversi fatti empirici. Ma un impoverimento di questo tipo è assolutamente contro l’atteggiamento psicologico e l’esperienza di lavoro di ogni scienziato.
Come diceva Whitehead, la scienza nasce da «una convinzione istintiva che esiste un ordine nelle cose o più precisamente un ordine nella Natura» e che questo ordine può essere compreso, almeno in una certa misura. 
L’atteggiamento ultimo di uno scienziato di fronte a un problema è di tipo conoscitivo ed è del tutto differente da quello di un ingegnere che deve realizzare una qualche macchina ed è ovviamente interessato alle nozioni scientifiche solo nella misura in cui esse possono essere utili al suo scopo. [Immagine a sinistra: Alfred North Whitehead (1861-1947)]
Di fatto, anche molti fra i maggiori esponenti del neopositivismo mutarono considerevolmente le loro posizioni negli ultimi anni della loro vita.
Tuttavia, se rifiutiamo lo strumentalismo e vogliamo assumere un punto di vista più realistico, siamo costretti a trovare un’altra via di uscita. Dobbiamo spiegare in qual preciso senso possiamo parlare di un progresso nella Fisica e quale contenuto di «verità» possiamo attribuire a una teoria che, noi sappiamo, prima o poi sarà trovata in contraddizione con nuovi fatti: capire in quale senso una vecchia teoria e le spiegazioni che essa dava di una classe di fenomeni possano rimanere valide all’interno di una nuova, quando anche i concetti basilari delle due sono completamente differenti.
In questo contesto penso possiamo superare molte difficoltà se conveniamo di attribuire in ogni caso alle teorie fisiche il significato di modelli, anche se di livello differente, e rinunciamo una volta per tutte all’idea che esse possano darci esplicita e in qualche modo diretta ed esaustiva conoscenza della realtà naturale.
Le teorie fisiche come modelli e l’evoluzione della Fisica
In relazione a quanto detto alla fine della sezione precedente, cerchiamo di chiarire brevemente il concetto di modello in Fisica e di capire le analogie e le differenze con il corrispondente concetto in Matematica. In Matematica usiamo il concetto di modello con riferimento a una ben definita classe di oggetti che soddisfano i postulati di una teoria astratta, secondo un preciso codice di traduzione o, che è lo stesso, una regola di corrispondenza biunivoca.
Per esempio, se associamo, secondo il solito metodo cartesiano, una coppia di numeri reali a ogni punto di un piano, un’equazione lineare a una retta, eccetera, otteniamo un modello della Geometria Euclidea (nel senso astratto inteso da Hilbert). Se, data una stella di rette nell’ordinario spazio euclideo, decidiamo di chiamare punto una retta, e retta un piano passante per il centro della stella, otteniamo un modello di Geometria Ellittica. 
Due differenti modelli della stessa struttura astratta possono avere una natura molto differente. Una coppia di numeri è assai diversa da qualsiasi realizzazione fisica dell’idea di punto. [Immagine a destra: David Hilbert (1862-1943)]
I ruoli dei punti e delle rette possono essere completamente scambiati nella Geometria Proiettiva, conducendo a due ben separati insiemi di affermazioni «duali». Ciò che è importante nel contesto è che qualsiasi teorema per il modello possa essere immediatamente tradotto in un teorema per la struttura astratta e viceversa.Così, comprendere un singolo modello equivale a comprendere la struttura astratta e ogni altro modello di essa.
L’uso del termine modello in Fisica è per alcuni aspetti analogo, ma per altri anche diverso. Noi usiamo in generale il termine modello con riferimento a una idealizzazione e a una forte semplificazione di una situazione complessa allo scopo di comprendere gli aspetti più importanti di un fenomeno, trascurando i particolari meno rilevanti. Tuttavia cosa è importante, e cosa è meno, o per nulla, rilevante, dipende dal contesto e dalla scala d’osservazione. Così possiamo dire che un modello è adeguato a una certa scala, o per un certo scopo, e inadeguato a un’altra scala o per un certo altro scopo. Se rappresentiamo idealmente i pianeti del sistema solare come punti materiali, otteniamo un modello che è perfettamente sufficiente per comprendere il moto dei pianeti rispetto al sole o il moto apparente del sole sullo sfondo delle stelle. Questo modello non è tuttavia sufficiente per spiegare l’alternarsi del giorno e della notte, il cambio delle stagioni, le fasi della luna. Per studiare questi fatti abbiamo bisogno di ricorrere al modello del corpo rigido per la terra e per la luna. Similmente, se vogliamo trattare con i complessi fenomeni che avvengono nell’atmosfera o sulla crosta terrestre, dobbiamo considerare in dettaglio la composizione chimica e le condizioni fisiche delle varie parti del nostro pianeta e i loro moti relativi.
Quello che è importante sottolineare, per il mio ragionamento, è che tutti questi modelli, che si suppone si riferiscano ultimamente allo stesso oggetto, sono disposti secondo una gerarchia. In relazione a un ben definito scopo, una volta che è raggiunto il livello adeguato della gerarchia, non guadagniamo nulla usando un modello di livello più elevato. Per quello che riguarda quello scopo specifico i due modelli sono completamente equivalenti, ci insegnano esattamente le stesse cose.
Mi sembra che, nell’ambito di questo discorso, possiamo comprendere in qual senso si può pensare che una teoria fisica sia in uno stato sempre provvisorio e incompleto e, nello stesso tempo, che ci insegni qualcosa che possiamo ritenere anche conclusivo sul mondo naturale. Se è vero che non possiamo pretendere che tale teoria ci dia una comprensione esaustiva del suo oggetto, tuttavia è innegabile che essa fornisce un «modello intelligibile» di validità potenzialmente permanente in un dato contesto.
Da questo punto di vista noi possiamo guardare senza difficoltà alle relazioni esistenti fra due diverse teorie, quando la seconda oltrepassa e include la prima. Possiamo pensare alla vecchia teoria come a un modello di livello gerarchico inferiore rispetto a quello nuovo, un modello che si applica solo in una situazione più particolare, ma che in tale situazione può persino essere più conveniente del nuovo, grazie alla sua maggiore semplicità. Come ci insegna la lezione dei modelli matematici, questi rimangono veri anche se le due teorie agiscono all’interno di strutture concettuali abbastanza diverse, naturalmente alla condizione che sia compreso il codice di traduzione appropriato.
Consideriamo qualche esempio. 
Per prima cosa prendiamo in esame l’idealizzazione dell’elettrone come punto materiale. [Immagine a sinistra: Paul A. M. Dirac (1902-1984)]
Questa idealizzazione rimane molto utile per descrivere il comportamento di questa particella in un campo elettromagnetico macroscopico ed è usata comunemente per progettare i nostri apparati sperimentali. Sarebbe insensato usare l’equazione di Dirac per il disegno di un acceleratore di particelle!
Alla luce della Meccanica Quantistica, tuttavia, il punto materiale è semplicemente una rappresentazione utile del pacchetto d’onda, quando è possibile trascurare la sua dimensione e il gradiente del campo al suo interno.
Una cosa simile si può dire del modello planetario dell’atomo, del modello di un cristallo come insieme di nuclei posti su un reticolo e di elettroni che si muovono al suo interno, o del modello di una molecola complessa costruito con piccole palline colorate.
Ciascuno di questi modelli ci permette di comprendere direttamente alcuni semplici fenomeni, come la distribuzione angolare delle particelle diffuse da una lamina sottile, la figura di diffrazione dei raggi X su un cristallo, le proprietà di sostituzione di un radicale organico. Essi contengono tuttavia informazioni molto importanti anche per la Teoria Quantistica. Possono infatti essere considerati come la codifica di un insieme di prescrizioni per scrivere le appropriate equazioni di Schrödinger o per scegliere l’appropriato insieme di soluzioni che sono necessarie per una comprensione di una più vasta classe di proprietà degli oggetti a cui si riferiscono.
Veniamo infine alla Teoria Quantistica dei Campi.
In questa teoria, parlare di particelle o di insiemi di particelle equivale semplicemente, come ho già accennato, a dare specificazioni sugli stati di certi campi. Ovviamente per comprendere il processo che avviene quando una particella accelerata ad alta energia colpisce un nucleo, o due particelle collidono tra loro all’interno di una macchina a fasci contrapposti, è necessario ricorrere a tutto il dispositivo della teoria.
Tuttavia, il modello classico di particella come punto materiale che percorre una traiettoria continua, risulta essere il più conveniente per descrivere i risultati finali e comprendere il significato dell’insieme di tracce che si formano, per esempio, in una camera a bolle. 
Allo stesso modo, se vogliamo studiare le proprietà dell’atomo di idrogeno, potremmo farlo utilizzando gli stati quantistici del campo elettronico, di quello protonico, e di quello elettromagnetico; ma, in una approssimazione non relativistica, il linguaggio dell’equazione di Schrödinger in termini di un elettrone e un protone come entità a sè stanti sarebbe molto più semplice e ci porterebbe allo stesso risultato. [Immagine a destra: Erwin Schrödinger (1887-1961)]
In conclusione mi sembra che la relazione di natura simbolica esistente fra due differenti modelli posti in una gerarchia, o fra due differenti teorie corrispondenti a un diverso livello della nostra comprensione, può essere essa stessa vista come un modello della relazione fra le nostre teorie fisiche e il mondo naturale che vogliamo studiare. Le idee che usiamo, i modelli, le teorie, sono costruzioni della nostra mente, ma non sono concetti vuoti di significato o arbitrari. Essi sono creati per comprendere la Natura e parlano di qualcosa a ogni stadio della nostra ricerca, anche se non sono mai completamente adeguati o non forniscono una comprensione esaustiva.
«O noi vogliamo specolando tentar di penetrar l’essenza vera ed intrinseca delle sostanze naturali; o noi vogliamo accontentarci di alcune affezioni. Il tentar l’essenza, l’ho per impresa non meno impossibile e per fatica non men vana nelle prossime sostanze elementari che nelle remotissime e celesti. […] Ma se vorremo fermarci all’apprensione di alcune affezioni, non mi par ci sia da disperar di poter conseguirle anco nei corpi lontanissimi da noi non meno che nei prossimi.» (Galileo, Terza lettera a M. Welser sulle macchie solari).
Giovanni Maria Prosperi
(Ordinario di Istituzioni di Fisica Teorica presso l’Università degli Studi di Milano)
Vai all’articolo in formato PDF
© Pubblicato sul n° 10 di Emmeciquadro
