Se si guarda la scienza non come una collezione di teorie e modelli teorici ormai consolidati dall’esperienza, ma come un’avventura in cui si arriva al risultato attraverso una serie di tentativi, ci si accorge che la costruzione di un modello, a partire dai dati a disposizione, è una vicenda che riveste un interesse conoscitivo, anche al di là della validità che solo a posteriori potrà essere verificata. Inoltre spesso questo lavoro di elaborazione produce strumenti di analisi che, oltre il destino del modello, sono successivamente utilizzati in altri ambiti di ricerca.
Un esempio di questo tipo è la teoria di James Jeans sull’origine del sistema solare, che rappresenta quasi un paradigma di come in un certo contesto, con certi dati a disposizione si può costruire una teoria rigorosa e coerente.
L’esperienza della ricerca scientifica
Il sapere scientifico è, alla base, ipotetico, si attua con il metodo sperimentale- matematico e il suo oggetto è il reale sensibile. Dal reale si estrae lo sperimentabile, con il ragionamento si sviluppa il pensiero interpretativo che coinvolge continuamente il confronto con il dato empirico. Poiché i dati empirici sono sempre in aumento, la scienza non è mai definitiva, ma sempre perfettibile. Ci troviamo di fronte a una via bella e luminosa, aperta e speculativa, lungo la quale si colgono i «veri», ossia «verità parziali», ma pur sempre verità.
Comunque l’idea stessa di spiegazione e di conoscenza scientifica, su base sperimentale, si fonda sulla «causalità» e sull’ordine temporale di «causa ed effetto».
Non è un caso che le leggi scientifiche siano matematicamente espresse nella forma di equazioni differenziali rispetto al tempo. Esse comprendono la nozione che una teoria generale spiega ciò che succede «adesso», nei termini di manifestazioni che avvengono nell’istante precedente o nel successivo. In accordo con l’ordine temporale causale solitamente risolviamo matematicamente tale equazione differenziale sulla base delle condizioni iniziali e in questo modo convertiamo la legge in un’ipotetica descrizione della storia che scorre dal passato verso il futuro.
Quindi un’equazione differenziale, che descrive un processo fisico, è spesso anche chiamata «modello matematico del processo». Nel costruire il modello matematico si deve ammettere un’abilità prerequisita che sorpassa la semplice osservanza di un protocollo di procedure. Cionondimeno può essere utile elencare alcuni gradini, o passi intermedi, che quasi sempre sono parte della costruzione del modello. Essi sono:
identificare le variabili principali e quelle secondarie;
ragionare attorno a un principio base che soggiace o governa il problema da affrontare;
esprimere matematicamente il principio, di cui al punto (2), in termini di variabili scelte al punto (1);
nella generalità dei problemi affrontati, il risultato del punto (3) è una equazione differenziale. Essa contiene il nocciolo del desiderato modello interpretativo.
Un’ulteriore barriera di difficoltà, caratteristica del problema teorico di James Jeans che andremo qui ad analizzare, è costituita dal fatto che esso appartiene all’insieme dei problemi cosiddetti dell’origine. Per esempio: origine dell’universo, origine della vita nell’universo, dell’uomo sulla terra… e altri consimili.
[A sinistra: James Jeans (1877-1946)]
Un approccio sistemico al problema ci dice che, conoscendo il sistema (sulla cui origine si indaga) all’epoca presente, desideriamo investigare sulla sua struttura all’epoca iniziale (cioè quella in cui si è originato). A partire da quest’epoca il sistema in istudio si è evoluto secondo certe modalità; come immediata congettura si suppone che questa evoluzione sia avvenuta spontaneamente.
Una successiva riflessione indica che questa parola «spontaneamente» significa semplicemente seguendo le leggi, oggi note, della natura. Ma ciò conduce all’interrogativo: chi ci assicura la costanza, ossia la permanenza di dette leggi? A dire il vero: nessuno!
Si tratta però dell’ipotesi più semplice … oppure anche di quella obbligata!
A ben vedere si ritorna a un principio, quello di «ragion sufficiente », che Wilhelm G. Leibniz pone alla base della sua filosofia. Assumiamo dunque l’ipotesi della permanenza delle leggi della natura, senza la quale non si può costruire nulla di teoreticamente valido e accettabile, a proposito di problemi dell’origine.
Il modello di cosmogonia del sistema solare
Il problema dell’origine del sistema solare ha affaticato, a partire da Cartesio, per lungo tempo e sino ai nostri giorni, la mente degli studiosi.
Per richiamare sinteticamente la posizione del problema esaminiamo innanzitutto l’insieme dei dati empirici, in questo caso osservativi (astronomici e astrofisici). Vediamo quindi le proprietà più salienti del sistema solare. Esse possono essere così riassunte. Vi è una stella in posizione centrale, il Sole, che è molto più massiccia della somma di tutte le altre parti del sistema.
Vi sono nove pianeti in orbite kepleriane con il fuoco coincidente con il centro del Sole.
Le orbite dei pianeti giacciono tutte assai vicino a un ben definito piano, in modo che il sistema planetario stesso è sostanzialmente bidimensionale.
Tutti i pianeti si muovono nello stesso senso, attorno al Sole, sulle loro orbite. Questo senso di rivoluzione, detto diretto, è quello che un ipotetico osservatore con i piedi sul Sole, constaterebbe come antiorario, mentre retrogrado (come quello di alcuni satelliti) è quello opposto.
Vi è una chiara distinzione nella composizione chimica dei pianeti, cui corrisponde sia una diversa collocazione spaziale (rispetto al Sole) sia diversi valori di massa e densità medie (Tabella I).
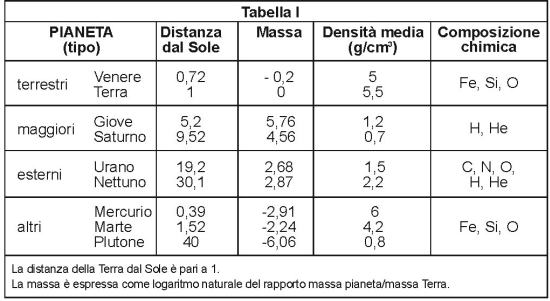
Vi sono anche numerosissimi oggetti più piccoli (asteroidi, comete, meteoriti, eccetera), la cui massa individuale è molto più piccola al confronto di quella dei nove principali pianeti e anche di quella dei satelliti.
In prima approssimazione i modelli, di natura astronomica e astrofisica, ossia le spiegazioni complessive che rispondono alla domanda: «come è stato originato il sistema solare?», sono raggruppabili in tre categorie:
il sistema planetario si forma da materia fornita dal Sole in conseguenza del passaggio di una stella ad esso vicina;
la formazione dei pianeti avviene, dopo che il Sole è già diventato una stella normale, mediante cattura di materia vagante nello spazio interstellare;
il sistema planetario è una diretta conseguenza della formazione del Sole. I due processi possono avvenire contemporaneamente o in successione.
Oggigiorno la soluzione del problema posto segue la via tracciata dalla categoria (c). Solo in questi anni, infatti, è possibile, mediante telescopi in orbita circumterrestre e altri strumenti di investigazione assai perfezionati, studiare accuratamente «sistemi planetari», attorno ad altre stelle, in statu nascendi. La ricerca, relativa a questo appassionante problema sarà ancora lunga e difficile: però permangono assai pochi dubbi sulla giustezza della direzione intrapresa.
Ai tempi di Jeans (vissuto tra il 1877 e il 1946) le categorie dei modelli si riducevano solo a quella (b), in quanto allora era generalmente adottata la teoria della nebulosa di Laplace con al centro il Sole. Essa peraltro, come già avevano notato nel XIX secolo scienziati come James C. Maxwell e Jacques Babinet, non era in grado di spiegare in quale modo la quasi totalità del momento angolare potesse essere devoluta a una frazione così insignificante della massa di un sistema isolato nello spazio. Ritorneremo comunque più avanti su questo concetto fondamentale. Nel 1916 Jeans presentò dunque un semplice ed elegante modello (per le vedute di quei tempi).
A grandi linee lo si può esporre nel seguente modo.
A causa di un passaggio di una stella in vicinanza del nostro Sole, l’azione gravitazionale di questo astro passante estrae dalla nostra stella, per una sorta di fortissima marea, una certa quantità di materia.
Questa forma allungata estratta, avente l’aspetto di un sigaro, diventa instabile meccanicamente ed entra in auto-oscillazione. Ciò conduce successivamente alla rottura che dà origine a una serie di globi. Questi ultimi, contraendosi formano i vari pianeti.
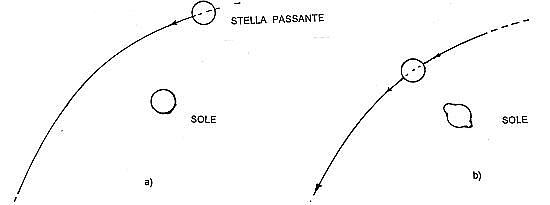
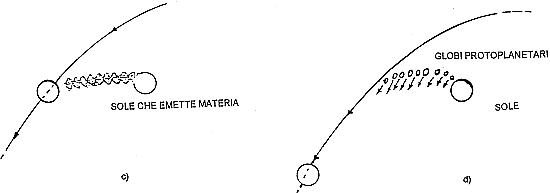
I quattro eventi principali della teoria di Jeans:
a) l’incontro con la stella passante;
b) la deformazione mareale del Sole;
c) l’emissione del materiale che entra in auto-oscillazione;
d) la formazione dei globi protoplanetari.
In conseguenza della configurazione iniziale del filamento estratto, i pianeti più massicci si troveranno al centro del sistema planetario e i meno massicci alle sue estremità (come in effetti si constata oggi nella disposizione dei pianeti). Il materiale residuo disperso costituirà una sorta di atmosfera diffusa, responsabile dell’azione mirante a rendere più circolari e quasi complanari le orbite iniziali dei protopianeti.
Jeans spiega la formazione dei satelliti attorno ai pianeti in questo modo: nei primordi di vita del sistema solare, quando le orbite dei pianeti erano ancora fortemente ellittiche, il protopianeta avrebbe subito, a sua volta e anche in misura maggiore o minore a seconda delle sue dimensioni, una parziale disgregazione mareale in concomitanza con il ritorno al perielio, sì da formare il sottosistema satellitario.
Dopo questa complessiva disamina del modello esplicativo di Jeans, ecco qualche commento che introduce alla successiva descrizione dei vari stadi costituenti il modello.
Con riferimento alle proprietà del sistema solare già viste, si può notare che si può ascrivere il principio di «estrazione mareale» all’intero modello; esso infatti informa sia la genesi dei pianeti sia quella dei satelliti.
Anzi questa ipotesi è assai interessante perché è proposta un’unica spiegazione concettuale dell’origine dei pianeti e di quella dei satelliti. Inoltre, si passerà, sia pure a grandi linee e in qualche dettaglio, alla applicazione matematica per rendere completa l’intera teoria.
Estrazione della materia dal Sole
Jeans investigò (1916-1917) in dettaglio l’interazione gravitazionale tra due stelle ravvicinate: la stella, per così dire predatrice o passante e quella vittima, cioè il nostro Sole.
Innanzitutto dimostrò che non è affatto necessaria una effettiva collisione al fine di rimuovere materia, trasferendola da una stella alle vicinanze di un’altra. Durante l’incontro ravvicinato la gravitazione causa il formarsi di un duplice rigonfiamento sulla stessa da cui è poi rimossa la materia.
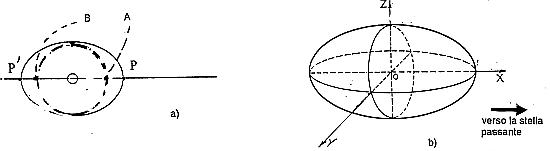
- Deformazione mareale causata sul Sole da una massa esterna; i rigonfiamenti massimi P e P’ sono in corrispondenza dei punti A e B
- Ellissoide a due assi, o sferoide, nello spazio.
In altre parole la stella vittima, il Sole, è dunque avvicinata da una stella predatrice che provoca, nel Sole, un cospicuo fenomeno mareale. Anziché conservare una forma pressoché sferica, il Sole assume allora quella di uno sferoide.
Con l’ausilio di una accurata trattazione matematica, Jeans trovò che, se l’eccentricità dello sferoide supera un certo valore, esso diventa instabile. Di conseguenza egli giunse alla conclusione che è possibile una perdita di massa.1
Instabilità della corrente fluida eiettata
Il materiale uscente dalla stella vittima, cioè il Sole, si presenta in modo disgregato e pertanto si può trattare, dal punto di vista del modello matematico, come una corrente fluida.
Trasferendo appunto questi concetti nel modello, Jeans dimostra che in questo flusso sorgono, per instabilità meccanica, onde e vibrazioni meccaniche simili a quelle che si stabiliscono, ad esempio, in una struttura meccanica come un filo teso oppure in una colonna d’aria nella canna di un organo.
Si può allora, spiegando in analogia e con termini semplici, studiare il processo oscillatorio proposto da Jeans al fine di comprenderlo più agevolmente. È ben noto il comportamento di un filo teso, fissato agli estremi.
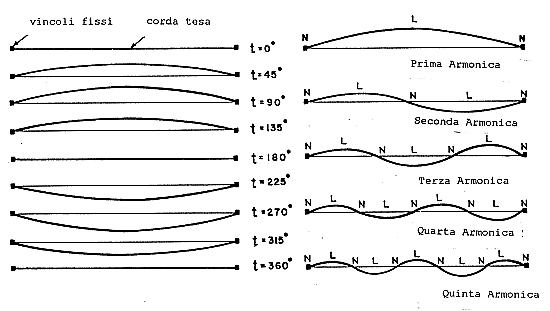
A sinistra: Corda tesa oscillante in fondamentale;
A destra: la stessa corda tesa oscillante anche in armoniche. N = nodo, L = ventre.
Come si vede nell’immagine a sinistra, una corda di violino, pizzicata a metà della sua lunghezza, vibra in risonanza fondamentale (o di prima armonica) assumendo le configurazioni illustrate nel diagramma (in vari istanti all’interno del periodo). Nell’immagine a destra si nota che, nel caso di risonanza di armonica superiore (seconda, terza …) ci sono punti in cui la vibrazione (in ogni istante) è massima, detti ventri e contrassegnati con L, e punti in cui essa è nulla, detti nodi N. Nel caso del violino, e di tutti gli altri strumenti musicali cordofoni, la vibrazione è trasversale. Negli strumenti aerofoni abbiamo invece una colonna d’aria in cui vi è una vibrazione longitudinale. In entrambi i casi vi è la sovrapposizione di un’onda acustica diretta e di una inversa; questa combinazione dà luogo all’onda stazionaria, come descritto nelle immagini di questa pagina.
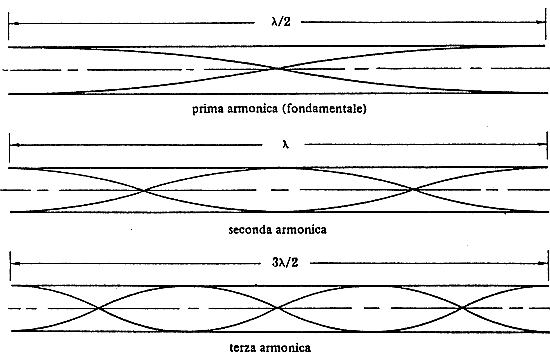
Modi di vibrazione di una colonna d’aria in un tubo aperto
Un’evidenza sperimentale, nel caso di onde stazionarie in un tubo pieno di gas, è realizzabile facilmente. Una sorgente di onde acustiche, per esempio un altoparlante posto in S, provoca le vibrazioni di un diaframma flessibile che chiude un’estremità del tubo.
Lo schema seguente illustra il fenomeno delle onde stazionarie: se la frequenza del suono è f, la sua lunghezza d’onda l e la velocità nell’aria è u, si ha che f λ = u.
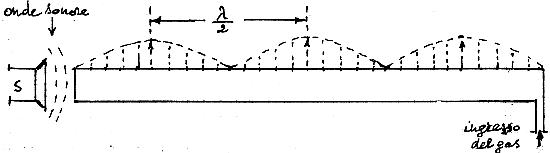
Si fa fluire gas illuminante (o da cucina) fino a riempire il tubo, attraverso un’apertura sulla parte inferiore del tubo stesso; da piccoli fori regolarmente distanziati e praticati sulla parte superiore, il gas fuoriesce lentamente. Il gas uscente viene acceso, in modo che si ha una serie di fiammelle.
Quando si alimenta l’altoparlante con un segnale, avente la frequenza per la quale la colonna d’aria è in risonanza, l’ampiezza dell’onda stazionaria diventa piuttosto grande e si può osservare la variazione dell’altezza delle fiammelle lungo il tubo.
L’intervallo fra nodi N e ventri (o antinodi) A è chiaramente osservabile nell’iimagine seguente.
Ritorniamo ora allo studio di cosmogonia planetaria di Jeans, in particolare all’oscillazione meccanica longitudinale del filamento estratto dal Sole.
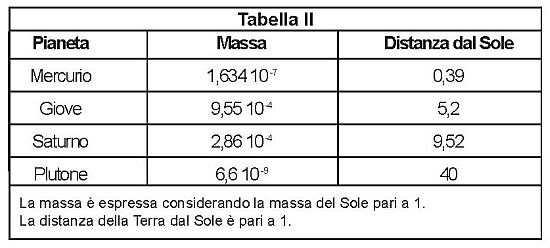
Qui la grandezza fisica che si propaga come onda, e determina la situazione di onda stazionaria, è la densità della corrente fluida che varia lungo il filamento, essendo massima nei ventri e minima nei nodi. In questa situazione Jeans dimostra che questo filamento può spezzarsi nei nodi dando luogo a globi discreti, destinati a crescere in massa e densità sino a costituire i protopianeti. Poiché la forma assunta, per il filamento eiettato, è quella all’incirca di un sigaro, i pianeti centrali saranno più massicci mentre quelli estremi, del sistema dei nove pianeti, i meno massicci.
La Tabella II mostra i valori attualmente noti delle masse planetarie in corrispondenza delle varie distanze dal Sole. Come si può notare, questa predizione è abbastanza verificata a fronte dei riscontri osservativi.
Riepilogo generale della teoria
La teoria mareale di Jeans è sintetica e per molti aspetti attraente a motivo della sua semplicità (l’apparato matematico per giustificarla è molto più complicato, ma di questo si parlerà più avanti).
A causa dell’azione gravitazionale di una stella di passaggio, il materiale è tratto fuori dal Sole in forma di una struttura filamentare. L’instabilità che sorge all’interno di questa corrente è responsabile della sua frattura in un certo numero di globi. Ciascuno di questi si evolve sino a costituire un protopianeta. Il materiale residuo, non aggregato e in prevalenza gassoso originario del filamento, poiché forma una sorta di atmosfera circumsolare, modifica a poco a poco le orbite primordiali rendendole sempre più circolari e complanari.
La formazione dei satelliti è congetturata, come prima abbiamo visto, secondo lo stesso sistema concettuale adottato per la formazione dei pianeti, sia pure in scala più piccola. Poiché le conoscenze sulla composizione chimica dei pianeti e dei satelliti erano, tra il 1916 e il 1930, assai scarse, la teoria di Jeans non prende posizione su questo argomento e ciò non causa difficoltà.
Partendo circa dal 1932 i ricercatori pongono obiezioni di fondo all’intero modello interpretativo o a parti di esso, tutto ciò verrà esaminato più avanti.
Luci e ombre della teoria
È fondamentale osservare che lo stato della ricerca, per quanto concerne gli studi sull’origine del sistema solare, tra il 1900 e il 1916, si trovava di fronte a una grande difficoltà. Il modello, universalmente accettato di Laplace, era ormai entrato in crisi da molti anni per la questione della distribuzione del momento angolare, già accennata.
[A destra: Pierre-Simon de Laplace (1749-1827)]
Datal’importanza dell’argomento, conviene approfondire un poco la questione. Il modello di Laplace, seppure migliorato con i raffinamenti matematici apportati da Henri Poincarè nel suo testo Leçons sur les hypotheses cosmogoniques del 1913, utilizzava una massa centrale e una atmosfera che la circondava ruotando, attorno all’asse passante per il centro della massa, con velocità angolare costante. Detto modello prevedeva l’espulsione successiva, attraverso il piano equatoriale del sistema isolato appena descritto, di opportuni anelli dai quali sarebbero poi originati i singoli pianeti.
Veniamo ora all’obiezione di Maxwell e Babinet. È ben noto, dalla meccanica razionale, che un sistema di masse ruotanti uniformemente (poniamo un disco) attorno a un asse, conserva la quantità meccanica detta momento angolare complessivo, qualora il sistema stesso sia isolato.
Nel caso di una sola massa il momento angolare è semplicemente dato dalla formula m v r, in cui m è la massa in discorso, v è la velocità tangenziale dovuta al moto rotatorio e r il raggio della circonferenza cioè l’orbita circolare della massa m nel suddetto moto rotatorio. Ovviamente nel caso di un insieme di masse con una certa distribuzione lungo lo sviluppo, per esempio di un disco, il calcolo del momento angolare è più complesso, ma sempre assimilabile al prodotto di una massa, di una velocità e di una opportuna distanza.
Ora l’osservazione astronomica, ossia il dato empirico di base, mostra un fatto a prima vista sconcertante. I pianeti di maggiore mole (Giove e Saturno), possiedono solo la frazione 1/740 della massa totale del sistema solare, ma hanno il 98% del momento angolare totale (ossia il loro prodotto m v r è quasi tutto il momento angolare, che deve essere costante perché il sistema solare è isolato); il Sole, che rappresenta quasi l’intera massa, è portatore solo del 2% del momento angolare totale.
Il modello di Laplace, quindi, sarebbe stato accettabile qualora avesse incluso un meccanismo di trasferimento del momento angolare, dal Sole ai pianeti, durante la formazione del sistema planetario stesso. Con la proposta rivoluzionaria di Jeans, sarebbe stato spiegato il puzzle del momento angolare cospicuo dei pianeti, causato dall’attrazione della stella passante che «strappava», per così dire, una piccola massa al Sole ponendola in orbita attorno a esso.
Alcuni osservatori, assai ironici, affermarono che Jeans «aveva gettato un sasso in piccionaia, in un luogo cioè frequentato da astronomi tranquilli». Certamente questa teoria mareale di Jeans ebbe una grande influenza e fu assai persuasiva in quegli anni.
Un altro aspetto interessante del modello è la sequenza dei passi successivi necessari alla sua costruzione, ossia quelli esposti nelle pagine precedenti. Esaminiamo ordinatamente i vari punti elencati.
In riferimento alla prima proprietà, si costituiscono come variabili principali quelle relative all’avvicinamento, della stella predatrice, al Sole mentre le secondarie sorgono di conseguenza; per la seconda proprietà, si pone come principio base la legge di attrazione newtoniana, per la terza viene sviluppato l’effetto conseguente alla attrazione gravitazionale, sia nella emissione di materia dal Sole sia nella formazione del filamento estratto.
Infine abbiamo il culmine dell’eleganza e del rigore del modello, nell’equazione differenziale che descrive la vibrazione nel filamento e il successivo spezzarsi di quest’ultimo per formare i pianeti (quarta proprietà).
Bellissima è poi la trattazione matematica dei singoli particolari fenomeni, come la condizione per l’espulsione della materia dal Sole. In questi calcoli Jeans ha impiegato una grandissima genialità nell’applicare le teorie delle armoniche sferiche. Mirabile è la signoria con cui l’astrofisico teorico tratta le funzioni speciali. Per quanto riguarda l’equazione differenziale che poi conduce allo stabilirsi delle onde stazionarie nel filamento, è assai utile, per la comprensione generale concettuale, l’analogia acustica riportata.
È giusto rivelare, in tutto questo quadro alcune «ombre» rilevabili nell’intera teoria. Innanzitutto il considerare, nel complesso scenario dei vari fenomeni fisici, solo le forze meccaniche: quella di attrazione e quelle dinamiche (dovute al moto). Tutto ciò in anni in cui l’astrofisica iniziava anche ad affrontare fenomeni concomitanti, come quelli termodinamici, radiativi e altri.
Poi anche il fluido considerato, per quanto riguarda il problema della fuoriuscita, per effetto mareale, dal Sole, è ritenuto quello ideale della fluidodinamica (cioè incomprimibile, non viscoso), astrazione utile solo in alcuni fenomeni di idromeccanica.
Obiezioni e superamento del modello
A partire dal 1932 i ricercatori posero alcune obiezioni di fondo, tali da compromettere la validità specifica dell’intero modello. F. Nolke studiò la stabilità dei globi planetari, all’atto della loro formazione dal filamento eiettato. 
Con opportuni calcoli dimostrò che i globi di materia, sottoposti all’azione mareale del Sole, non potevano consistere per autogravitazione e quindi era inevitabile la loro disgregazione. Nolke concluse che la teoria di Jeans poteva correttamente spiegare solo il formarsi di un involucro gassoso e polveroso attorno al Sole, non un sistema di pianeti.
Successivamente Henry N. Russell pose una serie di obiezioni, nella prospettiva tracciata da Nolke, relative alle distanze a cui si sarebbero formati i pianeti. Le sue conclusioni stabilirono che i pianeti non avrebbero potuto formarsi ad una distanza superiore a circa 5,8 milioni di km (dal Sole).
Più tardi, nel 1939, Lyman Spitzer, un pioniere per quanto concerne gli studi della fisica del plasma nel XX secolo, pose un’obiezione assai importante. Con un semplice calcolo egli dimostrò che un filamento di plasma, stato della materia di cui sono composte le stelle, estratto da un astro, non avrebbe avuto il tempo di raffreddarsi né quello per condensarsi ma, esplodendo, si sarebbe dissipato completamente nello spazio.
Un’osservazione a proposito di quest’ultima obiezione. Si tenga presente che la teoria di Jeans, essendo stata concepita tra il 1916-1920, non poteva prevedere il comportamento dei plasmi cosmici (le cui prime conoscenze sperimentali e teoriche sono da collocarsi dopo il 1935).
Ogni teoria fisica deve sempre essere valutata nel contesto culturale del tempo in cui essa è stata avanzata.
Importanza epistemologica del modello
In un interessante articolo del 1968 Tibor Herczeg così si esprimeva: «vi sono due direttive di ricerca in cosmogonia planetaria, fondamentalmente diverse. Esse si possono denotare: teorica ed empirica o, forse in modo più proprio, deduttiva e induttiva […] L’attitudine che possiamo chiamare puramente teorica può essere rappresentata dal famoso trattato Leçons sur les hypotheses cosmogoniques di Poincarè, oppure dalla ugualmente famosa teoria, ora superata, di Jeans dell’incontro ravvicinato stellare che dà origine all’evoluzione planetaria. Partendo da una generale ipotesi di lavoro, alcune teorie possono dedurre (o tentare di dedurre) la completa, più o meno dettagliata, storia dell’evoluzione del sistema fino a che esso ha raggiunto la forma presente […] Questo programma, mai completato con strumenti matematici, rappresenta il classico approccio al problema al fine di elaborare teorie, a partire dalla fine del XVIII secolo, sino al 1940 circa.»2
Il passo è senz’altro condivisibile, dal punto di vista epistemologico, specialmente in ordine alla teoria di Jeans. Quest’ultima infatti è in certo modo l’anello di congiunzione tra le teorie descritte nel trattato Leçons sur les hypotheses cosmogoniques e quelle apparse dopo il 1940. Pur essendo una teoria di natura ipotetico-deduttiva, ha proposto in modo rigoroso per la prima volta la soluzione dell’obiezione di Maxwell-Babinet.
Essa appartiene, tuttavia, alla famiglia delle «vecchie teorie» nelle quali la meccanica è studiata rigorosamente dal punto di vista della concettualizzazione delle grandezze in gioco e sviluppata con il calcolo in un modo esauriente. Altre parti del complesso problema cosmogonico però, che attengono ad altri settori della fisica, o sono ignorate o sviluppate in modo qualitativo, se non addirittura, in tutto o in parte, erroneo.
Non si tratta solo, come affermava Herczeg, di un approccio teoretico o matematico a fronte di un altro prevalentemente empirico, bensì di una mancata presa di consapevolezza, che si prolunga sino ai primi anni quaranta (e qui Herczeg ha perfettamente ragione), del fatto che, accanto ai fenomeni meccanici, vi sono molti altri fenomeni altrettanto importanti nello scenario complessivo relativo all’origine del Sistema solare.
Non vi è ombra di dubbio sul fatto che la teoria di Jeans, a partire dal 1939, sia stata superata dalle concezioni di Hannes Alfvén (effetti del campo magnetico primordiale sui plasmi cosmici) di Dirk Ter Haar e Gerard P. Kuiper (fenomeni termodinamici nelle fasi primordiali), Carl F. Weizsacker (dinamica dei fluidi primordiali e dei loro aspetti vorticali).
Da questi studi non si potrà più prescindere ed è appunto per questa via maestra che è proceduta la ricerca sino ai giorni nostri.
Considerazioni conclusive
Qui conviene porsi qualche interrogativo sul pensiero, in generale, dello scienziato Jeans.
Come mai un distinto ricercatore, autore di contributi originali e di avanguardia nei campi più svariati, dalla costituzione stellare alla teoria cinetica dei gas, dalla relatività alla quantistica e all’elettromagnetismo, abbia concepito una teoria sull’origine del sistema solare utilizzando oggetti concettuali, in fondo per il suo tempo, un po’ antiquati?
Tutto ciò insieme a un apparato matematico approfondito e di primo ordine e con un instancabile perfezionamento successivo durato circa quindici anni?
Una probabile risposta a questi interrogativi risiede forse nell’interpretazione seguente. Esistono settori diversi di speculazione, in un ricercatore scientifico, e in questi settori possono esservi squilibri di contenuti in ordine alla critica epistemologica. Inoltre vi sono poi delle pre-polarizzazioni psicologiche in certi argomenti. In altre parole è spesso necessario un tempo di incubazione psicologica per avere, solo per alcuni e determinati campi di ricerca, della consapevolezza per un corretto approccio scientifico di certi problemi.
Siamo comunque grati a Jeans di aver gettato, per così dire, un ponte tra ricerche del passato e quelle più avanzate che continuano fino ad oggi. E poi non dimentichiamoci che teorie attuali, come quella ad esempio delle onde di densità che ha gettato vivissima luce sulla comprensione della forma e dimensioni delle galassie a spirale, affondano le loro radici nello studio di Jeans dell’auto-oscillazione del filamento estratto dal Sole.
Vai all’articolo in formato PDF
Vittorio Banfi
(Ha collaborato, dal 1969 al 1984, presso l’osservatorio di Pino Torinese. Membro del centro di Astrodinamica G. Colombo. Dal 1987 collabora con il Dipartimento di Fisica-Matematica dell’Università. La sua ricerca si è sviluppata nel campo della astrofisica teorica del sistema solare e meccanica celeste classica e relativistica)
Vai all’Approfondimento: “Il Sistema Solare secondo J. Jeans”
Note
L’argomento è stato trattato da Jeans negli articoli segnalati in bibliografia.
T. Herczeg, Vistas in Astronomy, Pergamon Press, London 1968.
Indicazioni Bibliografiche
H. Poincarè, Leçons sur les hyphotheses cosmogoniques, Hermann, Paris 1911.
V. Banfi, Giornale di astronomia, 1-2, S.A.It., 1991.
J. Jeans, Mon, Not. R. Ast. Soc. 77, 1916, p. 84.
J. Jeans, Mon, Not. R. Ast. Soc. 77, 1917, p. 186.
J. Jeans, Mon, Not. R. Ast. Soc. 62, 1917, p.1.
J. Babinet, Comptes Rendus 52, 1861, pp. 481-484.
H.P. Berlage, The origin of the solar system, Pergamon Press, Oxford 1968.
F. Nolke, Mon, Not. R. Ast. Soc. 93, 1932, p. 159.
H.N. Russell, The solar system and its origin, Mc Millan, New York 1935. Tr. it. Il sistema solare e la sua origine, Mondadori, Milano 1941.
L. Spitzer, Astrophys. J. 90, 1939, p. 675.
T. Herczeg, Vistas in Astronomy, Pergamon Press, London 1968,10, pp. 175-206.
© Pubblicato sul n° 16 di Emmeciquadro
