L’articolo riprende un intervento tenuto in occasione della Convention Scuola 2016 dell’Associazione diesse (Didattica e Innovazione Scolastica), svoltosi a Bologna nel mese di ottobre 2016.
Per l’autore la matematica non è solo un linguaggio della Scienza, ma è anche un elemento costitutivo della conoscenza scientifica: «L’astrazione è un vero punto di forza che consente di raggiungere l’universalità nelle proprie conclusioni».
Ciò è vero non solo in matematica ma anche nella formulazione delle leggi teoriche della fisica.
C’è una conseguenza didattica: la relazione tra matematica e fisica diventa un elemento importante dell’insegnamento, è necessaria quindi una progettazione coordinata dei percorsi di insegnamento di queste discipline.
Vogliamo discutere il tema del linguaggio matematico nel suo nesso con le scienze, in particolare per quanto riguarda l’insegnamento scolastico. Questo nesso (se facciamo riferimento alle scienze insegnate a scuola) riguarda principalmente la fisica, quindi questo intervento riguarda principalmente l’insegnamento di matematica e fisica nella scuola secondaria di secondo grado.
Ho scelto comunque di mantenere il discorso il più possibile su un livello metodologico generale, nella speranza che queste riflessioni possano dare qualche spunto utile anche agli insegnanti di Scienze nella secondaria di primo e secondo grado.
Per impostare la questione partiamo da qualche autorevole affermazione.
[A sinistra: Richard Feynman (1918–1988)]
«La cosa strana della fisica è che anche per formulare le leggi fondamentali abbiamo bisogno della matematica. […] Più investighiamo, più leggi troviamo, più profondamente penetriamo la natura, più la malattia persiste: ognuna delle nostre leggi è un’affermazione puramente matematica. […] Voi mi potreste dire: “Perché non dirla a parole invece che a simboli? La matematica è solo un linguaggio, e noi vogliamo poterlo tradurre”. […] Ma io non credo che sia possibile, perché la matematica non è semplicemente un’altra lingua. La matematica è un linguaggio più il ragionamento; un linguaggio più la logica, cioè uno strumento per ragionare. In effetti, è una grande raccolta dei risultati dell’attento ragionamento di varie persone. Per mezzo di essa è possibile collegare un’affermazione a un’altra». (Richard Feynman, [4], pp. 43-44).
«È noto che lo studio matematico della natura ha avuto inizio nell’ambito dei fenomeni del moto (la meccanica) e, più in generale, dei fenomeni fisici. La matematica irruppe in questo contesto non come un semplice strumento pratico e ausiliario rispetto a degli obiettivi fondamentali della fisica che sarebbero stati definiti indipendentemente da esso. Nella formazione della meccanica, e più in generale della fisica, la matematica ha avuto un ruolo costitutivo». (Giorgio Israel, [5], p. XI)
In questi passi si afferma dunque: la relazione tra linguaggio matematico e scienza moderna non è accessoria; senza linguaggio matematico, la scienza moderna non esiste.
Cercheremo di documentare che è proprio così, ma anche di capire meglio «perché» è così, scoprendo che la matematica (che esisteva in forma matura già 2000 anni prima di Galilei) ha insegnato alla scienza moderna qualcosa di profondo che sta al cuore del metodo scientifico.
Il metodo scientifico e l’astrazione
Iniziamo richiamando qualche aspetto fondamentale del metodo della scienza galileiana. Paolo Musso (1964-…), nel suo saggio La scienza e l’idea di ragione [7], presenta in una sintesi significativa in quattro punti l’essenza del metodo scientifico così come viene concepito e fondato.
Il passaggio dal «tentar di penetrare l’essenza vera e intrinseca delle sostanze naturali» all’accontentarsi di «venire in possesso di talune loro affezioni», capovolgimento della scienza greca «a priori».
Le «sensate esperienze», ossia gli esperimenti mirati, contrapposti alla pura e semplice osservazione.
Le «dimostrazioni matematiche».
Il rifiuto del principio di autorità, conseguenza naturale dei tre punti precedenti.
Quindi, la scienza moderna nasce con un’operazione di autolimitazione: solo accettando di non occuparsi della realtà in toto, ma di certe specifiche proprietà («grandezze fisiche») si riesce a fare un discorso scientifico efficace.
Questa limitazione è molto più che un generico «limitarsi alla realtà fisica»: anche guardando una specifica «cosa» materiale, lo scienziato moderno osserva spesso pochi aspetti per volta, facendo astrazione da quanto non è sotto esame in quel momento.
L’oggetto dell’indagine scientifica è sempre (a dispetto della sua materialità) in un certo senso un oggetto astratto. Secondo il linguaggio di Evandro Agazzi (1934-…) [1], l’oggetto scientifico è ottenuto dallo scienziato ritagliandolo nella «cosa», secondo un particolare punto di vista.
Per esempio: in un esperimento meccanico, di un corpo che scivola su un piano inclinato, osservo le dimensioni, il peso, la superficie più o meno ruvida, ma difficilmente osservo la temperatura, la carica elettrostatica, per non parlare del colore, dell’odore, eccetera (tutte proprietà fisiche!). Di questo oggetto astratto si osservano alcune grandezze fisiche, pronte per essere descritte matematicamente.
Il passaggio dall’«esperienza» (osservazione di quanto accade in natura, in circostanze non create o volute da noi) all’«esperimento» (in cui le circostanze sono create e organizzate ad hoc da noi per includere certi fattori ed escluderne altri) è funzionale a questo passaggio dalla «cosa» reale all’oggetto dell’indagine scientifica.
La scienza dunque: delimita nella realtà il campo della propria indagine; ritaglia nella cosa l’oggetto di indagine, secondo un punto di vista particolare; studia oggetti astratti dalla realtà, pronti per essere descritti matematicamente.
C’è molta astrazione nella fisica, e non solo in quella moderna e oggettivamente molto sofisticata, ma anche in quella più basica:
Oggetti astratti (per esempio: cosa vuol dire «punto materiale»?);
Concetti astratti (per esempio: cosa vuol dire «forza»? È un concetto matematico astratto che entra come intermediario logico nelle leggi fisiche per tradurre la nostra idea di causalità; noi però osserviamo gli effetti delle forze, non le forze stesse);
Situazioni astratte (per esempio: «assenza di attrito», «caduta nel vuoto», «moto rettilineo uniforme»).
Dunque lo sguardo scientifico sul mondo osserva la realtà, ma al tempo stesso fa molta astrazione dalla realtà e nella realtà. Uno dei prodotti di questa astrazione è l’individuazione, «estrazione», «distillazione», dalla realtà complessa, di alcune grandezze fisiche, pronte per essere misurate, cioè tradotte in numeri.
Dal punto di vista didattico, all’inizio dello studio della fisica (nel percorso personale dello studente così come è stato nella storia), un problema di base è quello della delimitazione degli ambiti, della chiarificazione di che cosa stiamo parlando: gli oggetti, le situazioni e i concetti astratti, nel senso spiegato.
Astratti, cioè costruiti sì a partire dalla realtà, ma spogliando la realtà di tutte le proprietà tranne pochissime su cui concentriamo l’attenzione. Si fa fatica a insegnare e studiare queste cose, perché mentre si dice che si sta studiando la realtà, si parla di qualcosa che è molto lontano, se non a volte in apparente contraddizione, con l’esperienza quotidiana.
Occorre non nascondere ma affrontare di petto questo problema: non si capisce la scienza moderna se non si capisce che parla di oggetti astratti.
Ma allora non parla della realtà? Certo che ne parla, ma la realtà è complessa, e la storia ci ha insegnato che se vogliamo arrivare a capire la realtà complessa dobbiamo avere l’umiltà di partire dalle realtà più semplici, dai mattoni di base, dalle leggi di base, dai princìpi elementari, e questo significa fare molta astrazione rispetto al flusso della realtà fisica così come ci investe nell’esperienza.
Occorre osservare la realtà con un occhio critico che sa idealmente «sottrarre tutto tranne pochissimi elementi» alla realtà, per concentrarsi di volta in volta su un certo essenziale.
Si osserva con gli occhi e con molto ragionamento.
Il ruolo costitutivo della matematica nella scienza moderna
Si dice che la fisica studia, nella realtà, tutto ciò che è misurabile. Le grandezze fisiche vengono misurate, quindi tradotte in numeri (o vettori, o altre grandezze matematiche). La massa di un oggetto non è un numero, è una proprietà fisica di quell’oggetto; ma una volta misurata è tradotta da un numero, pronto per essere inserito in ulteriori calcoli ed equazioni.
La misurazione è la porta d’ingresso della realtà nella fisica; attraversata quella porta, la grandezza fisica è identificata con una grandezza matematica. E finché la realtà non attraversa quella porta, il gioco della scienza non può cominciare.
Osserviamo anche che mentre le grandezze fondamentali (tempo, lunghezza, massa, temperatura, eccetera) possono essere misurate, le grandezze derivate vengono calcolate a partire da grandezze primitive: velocità media = spazio/tempo; densità = massa/volume, eccetera. Notiamo che queste grandezze addirittura non potrebbero essere definite senza matematica.
Facendo un passo ulteriore, osserviamo che certe grandezze derivate sono definite con procedimenti matematici complessi. La velocità istantanea è la derivata della funzione «spazio percorso in funzione del tempo».
Questo non è un esempio qualsiasi: la scienza moderna nasce con galileo Galileo Galilei (1564-1642), ma matura con Isaac Newton (1642-1723), che le dà una forma più moderna grazie alla matematica che utilizza, il calcolo differenziale e integrale (e non solo).
Senza quella rivoluzione matematica che a fine 1600 viene compiuta con la nascita del calcolo infinitesimale, la scienza moderna sarebbe rimasta bambina. Addirittura, quindi, la scienza moderna non potrebbe esistere senza «una certa» matematica. 
[A destra: Giorgio Israel (1945-2015)]
Il fatto che le grandezze fisiche siano tradotte in grandezze matematiche è il presupposto dell’osservazione di Richard Feynman (1918–1988) da cui siamo partiti: ogni legge fisica è formulata in ultima analisi come relazione matematica (di solito un’equazione) tra grandezze fisiche (quelle che gli studenti chiamano «formule»). Non esiste altro linguaggio.
Dovrebbe risultare evidente ora la verità dell’affermazione di Giorgio Israel (1945-2015): la matematica non si inserisce come uno strumento in più nello sviluppo della scienza moderna, come se questa preesistesse; al contrario, la matematica gioca un ruolo «costitutivo» nella scienza moderna.
Attenzione: non stiamo dicendo con queste affermazioni che la fisica «si riduce» alla matematica, che la fisica è «solo» matematica. Stiamo dicendo che la matematica è un organo vitale dell’organismo che chiamiamo fisica, senza il quale l’organismo non può neppure nascere.
Che poi la necessità di insegnare certi concetti ad allievi che non possiedono ancora la matematica necessaria possa indurre l’attitudine ai «giri di parole» (per evitare il più possibile la matematica), questa è un’altra questione, ma dobbiamo arrenderci alla realtà: il linguaggio naturale della scienza moderna è la matematica, anzi «una certa» matematica, quella da Newton in poi.
Astrazione e universalità, in matematica e in fisica
Fermiamoci ora per un momento in questa analisi del metodo scientifico e della matematizzazione della fisica, e passiamo a considerare il metodo della matematica in se stessa.
Utilizziamo come esempio guida per le nostre osservazioni il caro vecchio teorema di Pitagora: «In un triangolo rettangolo, il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti». Per quello che mi interessa osservare bastano le prime parole: «In un triangolo rettangolo… ».
Cosa vuol dire? Significa «In un “qualsiasi” triangolo rettangolo…». Dunque il teorema parla di infiniti triangoli rettangoli e afferma che in uno qualsiasi di questi vale una certa proprietà. Ogni volta che vale l’ipotesi (il triangolo è rettangolo) vale la tesi (il quadrato dell’ipotenusa è…).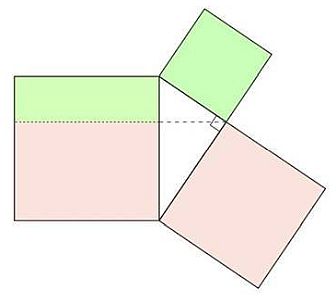 
Dunque il teorema di Pitagora contiene infinite affermazioni.
E come facciamo a sapere che è vero? Perché ne conosciamo una dimostrazione: è questa a convincerci oltre ogni ragionevole dubbio che il teorema vale.
Riflettiamo sulla potenza del metodo matematico: con un numero finito di passi del ragionamento ci convince della verità di infinite proprietà.
Com’è possibile? Certamente non esaminando uno per uno gli infiniti triangoli rettangoli esistenti e constatando che la proprietà è vera: non finiremmo mai. Il metodo matematico non è la constatazione caso per caso, ma la dimostrazione, che raggiunge l’universalità che sarebbe impossibile col primo metodo.
Come procede la dimostrazione? Si considera un «generico» triangolo rettangolo, e si mostra che necessariamente il quadrato costruito sull’ipotenusa ha certe proprietà.
Ma cosa vuol dire «si considera un generico triangolo rettangolo». Non che se ne prende a caso uno particolare e si lavora con quello, ma che si fa un ragionamento in cui ogni passo si appoggia solo sulla definizione di triangolo rettangolo (o sulle conseguenze logiche di questa definizione), cioè sulle proprietà che valgono per ciascun triangolo rettangolo, indipendentemente da quale abbiamo scelto. Ma questo è possibile perché «triangolo rettangolo» è un concetto astratto, definito da poche proprietà. La genericità è resa possibile dall’astrazione dell’oggetto di cui si parla.
Quindi: la potenza del metodo dimostrativo matematico, che è l’arma specifica, caratteristica, di quel metodo di conoscenza che chiamiamo matematica, consiste nella capacità di ottenere verità universali (cioè riguardanti infiniti oggetti) in modo unanimemente condiviso; e questo è reso possibile dalla natura astratta dei suoi oggetti. L’astrazione degli oggetti matematici rende possibile un ragionamento dalle conclusioni universali.
Dopo questa digressione sul metodo matematico, possiamo ora tornare al metodo scientifico.
Cosa fa lo scienziato quando, mediante riflessione, esperimenti e dimostrazioni, stabilisce una nuova legge fisica?
Stabilisce (o almeno: ambisce a stabilire) una verità universale: una verità che riguarda infiniti oggetti o fenomeni. La legge di gravitazione universale non serve a dirci che fino a oggi le mele sono cadute in un certo modo, pretende di dirci che cadranno così anche domani. 
[A destra: Karl Popper (1902-1994)]
Il punto è: come fa lo scienziato a stabilire che è così? Se si trattasse di moltiplicare indefinitamente le constatazioni delle regolarità di fatto, non finiremmo mai di constatare, e non potremmo mai concludere nulla di universale, come già osservava criticamente Karl Popper (1902-1994): «Per quanto numerosi siano i casi di cigni bianchi che possiamo aver osservato, ciò non giustifica la conclusione che tutti i cigni sono bianchi» (v. [8], p. 6).
Popper (implicitamente) riteneva che la scienza non abbia altre armi rispetto all’indefinita ripetizione dell’esperienza del constatare regolarità di natura, e ne concludeva l’impossibilità di stabilire qualunque legge universale: ogni affermazione scientifica è eternamente falsificabile. Io credo che la pratica scientifica consista in ben altro rispetto a questa iterata constatazione.
Riflettiamo sulla tecnica dell’«esperimento». Ha una profonda analogia con il metodo della dimostrazione matematica: non si considerano uno per uno tutti i triangoli rettangoli, si considera il triangolo rettangolo generico.
Cosa fa uno sperimentatore? Non considera uno per uno tutti i possibili pesi che possono scivolare su un piano inclinato, considera un peso generico.
Questo ovviamente non è possibile nello stesso senso in cui è possibile in matematica, tuttavia le condizioni controllate di laboratorio (eliminare gli elementi di disturbo, ridurre per quanto possibile l’oggetto reale a oggetto astratto caratterizzato da poche grandezze fisiche significative) e la ripetizione delle prove in modo limitato ma con una variazione mirata e significativa dei parametri in gioco, cercano di ricreare le «condizioni di genericità», cercano di approssimare nella realtà il concetto di «oggetto generico».
Il metodo della scienza moderna cerca quindi di stabilire leggi universali con un metodo che ha una profonda analogia (non dico identità, sia chiaro) con il metodo dimostrativo matematico: lavorando sulla realtà con oggetti «resi astratti» dal punto di vista scientifico, cerca di approssimare il concetto di «oggetto generico» per tentare una dimostrazione generale dei propri asserti, che ambiscono a essere «implicazioni universali», un po’ come i teoremi matematici.
Di nuovo, l’astrazione degli oggetti rende possibile un ragionamento di conclusioni universali.
Per la matematica come per la scienza, possiamo dire che l’astrazione è un vero punto di forza, che consente di raggiungere l’universalità nelle proprie conclusioni.
Nel caso della scienza, che ambisce a descrivere e comprendere la realtà fisica, questo è un apparente paradosso: per comprendere la realtà, dobbiamo a volte allontanarci da molta realtà, e concentrarci solo su pochi aspetti. Ma questo metodo è un ingrediente non secondario della lezione di Galileo.
Insegnare una disciplina, insegnare cos’è una disciplina
Credo che qualsiasi insegnante, se è appassionato alla sua disciplina, insegnando a qualsiasi livello, non vuole trasmettere solo un po’ di quella disciplina (cioè: alcuni contenuti della disciplina stessa), ma vuole anche insegnare un po’ di «cos’è» quella disciplina, quali sono i suoi obiettivi e metodi caratteristici.
Nell’insegnamento noi vogliamo dare delle chiavi di lettura della realtà e delle chiavi di lettura della cultura. Se uno studente di liceo ha già deciso che all’università farà giurisprudenza o lettere, cosa gli serve studiare matematica, fisica, chimica,…? Forse certi contenuti specifici gli serviranno poco, ma se diventa grande avendo qualche idea corretta su cos’è la scienza e cos’è la matematica, questo è apprezzabile: è un atlante mentale che gli darà una maggior capacità di comprensione e rapporto con persone e aree della cultura lontane dalla sua. Se poi trattiene criticamente anche certi contenuti, avrà una chiave di lettura in più della realtà attorno a sé.
Se, allora, abbiamo compreso che la matematica gioca un ruolo costitutivo nella scienza moderna, comunicare questo aspetto, documentare, esemplificare la relazione tra matematica e fisica diventa un obiettivo rilevante dell’insegnamento sia della matematica sia della fisica.
Questa è una delle «grandi idee di fondo» da passare. È importante comunicare quest’idea.
Perché spiega meglio «cos’è» la scienza e cos’è la matematica (il ruolo «costitutivo» di cui abbiamo parlato).
Perché è una motivazione forte allo studio della matematica delle scuole secondarie (e quanto c’è bisogno di motivazioni nello studio della matematica!).
Perché fa capire meglio sia la matematica sia la fisica, aiuta a rendere lo studio di entrambe più ragionato, meno meccanico, meno mnemonico.
Il linguaggio matematico come portatore di conoscenza scientifica
Abbiamo visto che l’oggetto fisico è descritto da alcune grandezze fisiche, che a loro volta sono descritte da grandezze matematiche o addirittura definite mediante procedimenti matematici; queste grandezze matematiche poi entrano nelle equazioni che esprimono relazioni fisiche o leggi fisiche. A questo punto le equazioni possono essere combinate ottenendone di nuove: per via puramente matematica otteniamo così delle conclusioni aventi significato fisico.
La scienza, diceva Galilei, procede attraverso «sensate esperienze e matematiche dimostrazioni». Queste sono le due gambe attraverso cui la conoscenza scientifica procede. È importante cogliere il valore di questo aspetto, perciò vediamone alcune sfaccettature.
Anzitutto: quello che viene chiamato «linguaggio matematico» (a volte in modo intenzionalmente riduttivo, come se la matematica fosse «solo un altro modo di dire le cose») è molto più di questo: la matematica è un metodo di conoscenza. Una deduzione logica, nella misura in cui ci fa pervenire a una conclusione di cui non eravamo già consapevoli, aumenta effettivamente la nostra conoscenza.
Il fatto che la conclusione fosse «implicita» nelle premesse non toglie il fatto che senza il lavoro dimostrativo non sarebbe emersa alla nostra consapevolezza; perciò la conoscenza è aumentata [2].
Si può anche dire: il linguaggio matematico è un modo sintetico di dire le cose, che incorpora in sé a volte secoli di pensiero e di progressi; perciò se una volta tradotto un problema verbale in linguaggio matematico questo appare banale, non vuol dire che era già banale prima: vuol dire che la matematica è potente [3].
Quando questo metodo deduttivo viene applicato a premesse aventi contenuto fisico, la conclusione fa aumentare le nostre conoscenze fisiche. La matematica è quindi uno dei metodi (non l’unico, certo!) con cui aumenta la conoscenza scientifica. Gli altri sono l’esperimento e la riflessione (attorno a esperimenti, fenomeni, teorie, deduzioni…).
Se siamo consapevoli di questo, e se nell’insegnamento scientifico vogliamo, come si diceva, non solo comunicare un po’ di scienza, ma anche comunicare un po’ di che cos’è la scienza, allora nell’insegnamento delle scienze a scuola dovranno trovare posto «Sensate esperienze e matematiche dimostrazioni».
Mostrare qualche significativa deduzione matematica di nuove leggi fisiche a partire da altre già accettate è istruttivo ed esemplare tanto quanto mostrare in laboratorio qualche esperimento significativo che vada alla radice delle leggi fisiche che si stabiliscono dall’osservazione sperimentale.
La progettazione del percorso di insegnamento
Il fatto che mostrare il ruolo della matematica nelle scienze sia riconosciuto come un obiettivo importante implica che a questo obiettivo vanno anche orientate e subordinate altre scelte didattiche.
Una prima conseguenza è che è necessaria una progettazione coordinata dei percorsi di insegnamento di matematica e fisica. Quest’affermazione sembra ovvia, ma non è sempre realizzata, perché a essa si oppongono altre esigenze didattiche, di per sé legittime.
Subordinare le scelte di percorso didattico, nell’insegnamento di matematica e scienze, al mostrare l’utilizzo della matematica per deduzioni fisiche, implica una serie di scelte nella progettazione di entrambi i percorsi in cui l’esempio significativo, l’argomento esemplare, ha un’importanza a cui vale la pena di sacrificare la sistematicità a tutti i costi, l’organicità e la linearità del percorso a tutti i costi.
Un esempio: tra la fine della scuola media e il biennio delle superiori si svolge la delicata introduzione dell’algebra, calcolo letterale, equazioni, eccetera Il tutto viene fornito con una certa sistematicità e con somministrazione di esercizi tecnicamente elaborati, con l’esito che i primi concetti elementari sulla manipolazione di un’equazione di primo grado vengono introdotti sempre troppo tardi, rispetto all’utilità che questi avrebbero già più precocemente, nel manipolare semplici formule in geometria (aree, volumi) o in scienze.
C’è sempre un’età in cui allo studente è di fatto richiesto di saper «rigirare una formula» senza che nessuno gli abbia veramente spiegato come si fa e perché. Questo rischia di arrecare un danno duraturo: si moltiplicano le cose che lo studente impara a memoria, si perde l’occasione di mostrare come la matematica sia d’aiuto e non d’inciampo, non si educa l’idea che «ragiona, e capirai come si fa».
D’altro canto, l’insegnante dovrebbe accettare il fatto che insegnare a manipolare un’equazione ax = b non significa necessariamente aprire un lungo periodo in cui si risolveranno equazioni di primo grado sempre più complicate. Per ciò che serve alla geometria e alle scienze, bastano davvero i primi concetti, ma quelli andrebbero dati presto e bene.
Un discorso analogo si può fare con i primi rudimenti di trigonometria, cioè l’utilizzo delle funzioni seno e coseno per la risoluzione dei triangoli rettangoli. Cose che risultano ben presto utili, e che non implicano necessariamente una lunga permanenza sulle identità trigonometriche; queste si possono rimandare.
Altro discorso va fatto per il calcolo differenziale, richiesto ora in tutti i licei, all’ultimo anno.
Occorre ripensare i percorsi in vista degli obiettivi: in un liceo classico gli elementi di calcolo differenziale utili alla fisica di base e ai problemi di ottimizzazione (che sono le motivazioni per cui questi elementi sono stati introdotti nelle indicazioni ministeriali) non possono essere sviluppati «dopo» tutta la teoria dei limiti tradizionalmente sviluppata nei licei scientifici. La definizione di limite finito al finito dev’essere data per introdurre immediatamente la definizione di derivata, che è il vero protagonista del calcolo differenziale.
Questi sono solo pochi esempi, occorre realmente riprogettare le scansioni temporali dei singoli argomenti matematici anche in vista del loro utilizzo.
Un’osservazione complementare è la seguente. Per quanto si cerchi di progettare percorsi sensati, rimane vero che la matematica che «servirebbe» per la fisica, a ogni livello del percorso scolastico, è sempre di più di quella che si sa già: la prima lezione di cinematica richiederebbe già la derivata.
Questo suggerisce, allora, di considerare la possibilità di rivedere in una classe successiva un argomento più elementare di fisica, che solo ora – con la matematica a disposizione – può essere rivisitato con un certo valore aggiunto.
Un esempio: di moto circolare uniforme e moto armonico si parla prima della quinta liceo, ma se in quinta liceo conosciamo le derivate delle funzioni seno e coseno, possiamo ritornare sulla matematica del moto armonico, ottenendo due scopi: una comprensione più sintetica, concettuale, del moto armonico; una motivazione in più sul perché in analisi si studiano le funzioni trigonometriche.
Altro esempio: rivisitare il concetto di lavoro dopo che si è parlato di integrale, e riottenere il lavoro come integrale della forza nello spostamento, in qualche caso di forza non costante. (Per esempio: lavoro per allontanare un punto materiale in un campo gravitazionale).
Questo genere di rivisitazioni può essere apprezzato anche dallo studente, a condizione che l’argomento studiato «in passato» sia percepito come «una cosa facile» e non come «una cosa dimenticata».
Questa è una delle sfide dell’insegnamento delle materie scientifiche: far capire che, se lo studio è ragionato, l’apprendimento può essere cumulativo, anziché secondo il triste schema «cosa nuova imparata implica cosa vecchia dimenticata».
Marco Bramanti
(Professore ordinario di Analisi Matematica, presso il Politecnico di Milano)
(Questo testo è estratto da quello preparato per l’intervento tenuto dall’autore in occasione della Convention Scuola 2016 dell’Associazione diesse, teamwork “Il cantiere delle scienze” sul tema Lingua e linguaggi nell’insegnamento / apprendimento delle scienze, Bologna, 22/10/2016)
Note bibliografiche
E. Agazzi: Temi e problemi di filosofia della fisica, Manfredi, 1969.
M. Bramanti: Elogio dell’astrazione. L’interesse degli oggetti matematici. Parte 1°: Emmeciquadro, n° 49 – giugno 2013; Parte 2°: Emmeciquadro, n° 50 – settembre 2013.
M. Bramanti: I linguaggi matematici: idee e simboli. Parte 1°: Emmeciquadro, n° 42 – agosto 2011; Parte 2°: Emmeciquadro, n° 43 – dicembre 2011.
R. Feynman: La legge fisica (1965), Boringhieri 1971.
G. Israel: La visione matematica della realtà, Laterza, 2003.
R. Manara: La matematica e la realtà. Linee di metodo, Marietti, 2002.
P. Musso: La scienza e l’idea di ragione. Scienza, filosofia e religione da Galileo ai buchi neri e oltre. Mimesis, 2011.
K. R. Popper: Logica della scoperta scientifica, Einaudi, 1970.
© Pubblicato sul n° 63 di Emmeciquadro
