In un recente articolo apparso su Nature si commentano i dati di un esperimento molto interessante sotto diversi punti di vista. Il tema di base è quello del collasso di un sistema e dei ‘segnali’ che lo precedono. Sono alcuni anni che la ricerca si interessa alla definizione dei comportamenti tipici (e indipendenti dal particolare sistema studiato) in vicinanza di una ‘catastrofe’, di una brusca transizione cioè che porti il sistema verso un diverso regime di funzionamento o addirittura verso la scomparsa. Qualunque sia il sistema studiato (attività elettrica di reti neuronali nelle vicinanze di una crisi epilettica, comportamento delle quotazioni dei titoli in borsa prima di un crollo, andamento dei parametri cardiovascolari in prossimità di un infarto, andamento dei parametri chimico-fisici in un reattore vicino ad un’esplosione…), il comportamento comune è quello di un deciso aumento dell’entità della correlazione tra le parti del sistema, seguito da una grande volatilità (aumento brusco delle fluttuazioni dei parametri definenti il sistema).
In un bellissimo articolo del 2010 veniva riportano il grafico esplicativo riportato a fondo pagina di ciò che accade a un sistema sottoposto a uno stress che può (eventualmente) portarlo verso la catastrofe. Nel pannello di sinistra viene schematizzato un sistema nel suo stato normale (Comfort): i simboli indicano diverse ‘realizzazioni’ del sistema: come configurazioni a differenti istanti di tempo (variabilità temporale) o diverse repliche dello stesso sistema (variabilità spaziale); gli assi indicano due parametri rilevanti per lo stato generale: come pressione e temperatura di un sistema termodinamico, pressione e frequenza cardiaca, concentrazioni di differenti specie chimiche, quotazioni in borsa di due titoli… La resa grafica ci impone di considerare uno spazio bidimensionale ma nei sistemi reali le variabili che descrivono lo stato del sistema possono essere anche molte di più.
La situazione di Comfort è caratterizzata da un gioco ‘libero’ del sistema (le variabili sono indipendenti, le configurazioni ammesse occupano uniformemente lo spazio) all’interno di uno spazio relativamente ristretto (indicato da una circonferenza) di valori normali dei parametri. Muovendoci verso destra (freccia in alto), quindi andando verso ‘il peggio’ sotto l’azione di un fattore di Stress, si osserva una decisa deformazione dello spazio delle fasi che diventa molto più correlato; i parametri non hanno più la possibilità di un gioco indipendente ma sono vincolati a muoversi di concerto: la fluttuazione di una variabile provoca modificazioni nelle altre. Gli autori offrono un quadro molto convincente di questo comportamento, riportando il netto aumento delle correlazioni statistiche tra i descrittori di vari sistemi sottoposti a stress.
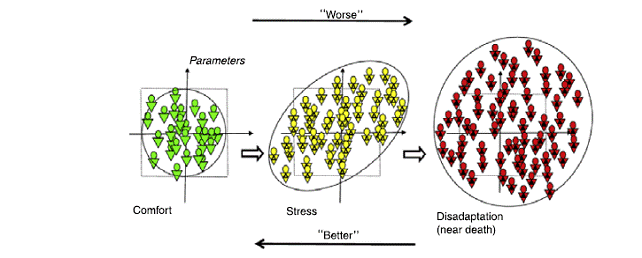
Arrivati in prossimità del punto di catastrofe (terzo pannello), il sistema occupa uno spazio molto più grande di quello iniziale, le correlazioni si perdono e al loro posto subentra un netto aumento di volatilità, cioè dell’entità delle fluttuazioni, schematizzato in figura con l’allargamento della zona occupata dal sistema nella condizione indicata come Disadaptation.
A questo punto si aprono due possibilità:
A) il sistema giunge a morte (o va verso un regime completamente differente come nelle transizioni di stato della materia: ebollizione, liquefazione…);
B) il sistema recupera il suo stato iniziale e nel farlo (freccia in basso) ripercorre la condizione intermedia ad alta correlazione, come se ci fosse bisogno di ‘riallacciare i rapporti’ fra le sue parti per ristabilire una situazione di equilibrio.
L’universalità della dinamica descritta deriva dall’universalità del concetto di rete: ogni sistema può essere immaginato come costituito da parti in relazione fra di loro e lo studio dell’entità delle relazioni fra le parti costituisce il punto di vista più informativo sul suo comportamento. Questa considerazione è alla base del profondo cambio di paradigma che sta investendo tutta la scienza: il livello privilegiato per le spiegazioni non è più quello microscopico – in cui avvengono le relazioni causali rilevanti essendo gli strati più macroscopici dei puri epifenomeni di leggi situate a un livello fondamentale (riduzionismo, approcci bottom-up) – e neanche quello macroscopico, da dove leggi molto generali determinano a cascata il comportamento dei livelli inferiori (olismo, approcci top-down).
Ciò che si profila è una sorta di approccio “middle-out” (o mesoscopico), in cui il livello più rilevante per la spiegazione è quello che permette la vista più completa delle relazioni intercorrenti fra le parti del sistema. In termini metaforici è come se, per caratterizzare lo stile di una cattedrale medievale, piuttosto che considerare la pianta generale dell’edificio (approccio top-down) o il materiale da costruzione (approccio bottom-up), ci concentrassimo sulla forma degli archi (approccio middle-out), essendo l’arco l’elemento privilegiato di raccordo fra le parti.
Nell’articolo di Nature citato all’inizio, gli autori esplorano una dimensione particolarissima della dinamica generale qui brevemente descritta, che ha delle implicazioni rilevanti in termini sia biologici che più generalmente epistemologici.
Il sistema sperimentale preso in considerazione è la crescita di popolazioni di Saccharomyces cerevisiae (il comunissimo lievito di birra) in coltura: da popolazioni di lievito cresciute in laboratorio vengono quotidianamente estratte frazioni variabili di cellule che poi vengono messe a crescere in un mezzo fresco. Le cellule di lievito si nutrono in maniera cooperativa condividendo tra di loro i prodotti dell’idrolisi dei nutrienti primari (in questo caso il saccarosio); ciò fa sì che, se si semina un numero troppo esiguo di cellule in un ambiente di coltura troppo vasto, la popolazione non riesce ad auto-sostenersi e va incontro alla morte.
Nelle condizioni descritte nell’articolo, la diluizione più alta che si può ottenere avendo una fondata speranza di cooperazione e quindi di raggiungimento di una situazione stabile della colonia corrisponde a una frazione pari ad 1/1700 della popolazione iniziale. Diluizioni più elevate non permettono quasi mai la successiva sopravvivenza, mentre diluizioni meno estreme (e.g. 1/500, 1/1000) solo raramente vanno incontro ad estinzione. Notiamo subito che qui a ‘fare rete’ sono le singole cellule di lievito, che stabiliscono una sorta di primitiva società di cellule che garantisce la sopravvivenza dell’intera popolazione; e già da questo primissimo punto ci accorgiamo come il concentrarsi della quasi totalità della ricerca biologica sui processi che avvengono all’interno della singola cellula costituisca un gravissimo errore di prospettiva. Ma andiamo avanti.
Gli autori, in accordo con lo schema che abbiamo riportato in figura, registrano le attese modificazioni in termini di aumento di correlazione e successivo aumento di volatilità nei parametri di crescita delle colonie di lievito nell’intorno della diluizione critica. Questo vale per colture isolate; in altre parole, per uno schema in cui la stessa cultura madre viene successivamente campionata per dar vita alle culture figlie ad alta diluizione, il raggiungimento del valore numerico della popolazione madre da parte della coltura figlia è indice del completo recupero (il tempo di recupero è circa una settimana), l’estinzione della colonia figlia è indice di avvenuta catastrofe.
Cosa avviene se si introduce una (apparentemente piccola) variazione a questo schema di base ? La variazione introdotta dagli autori è stata quella di procedere in parallelo con diverse colture in cui si operava lo stesso procedimento e di mescolare tra di loro le frazioni provenienti da colture madri differenti, la figura (tratta dall’articolo di Nature) riporta lo schema sperimentale adottato:
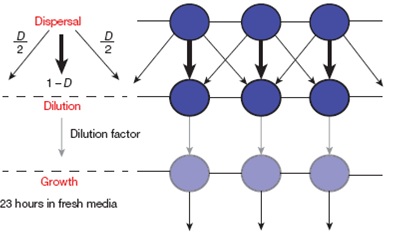
Le frecce sottili indicano la diluizione di due frazioni di eguale numerosità (D/2) provenienti da due colture madri diverse (cerchi viola scuro) e fatte poi crescere nel mezzo fresco a bassa densità (freccia ‘Dilution factor’) corrispondente al cerchio pervinca.
Questo cambiamento di paradigma sperimentale provoca una perdita netta dei ‘segni premonitori’ classici della vicinanza al punto di catastrofe: anche se poi alcune colture figlie andranno incontro a morte, prima dell’estinzione non mostreranno, se non in minima parte, i consueti segni di aumento di correlazione e di variabilità. Gli autori notano questo cambiamento e si concentrano su altri segni che invece permangono e con cui giudicare la presenza di una situazione critica e precisamente (nel caso ovviamente in cui la popolazione ‘ce la faccia’) l’allungamento del tempo di recupero e, cosa ancora più importante dal punto di vista pratico, l’allungamento dello ‘spazio di recupero’, cioè dell’area della coltura in cui la perturbazione mostra i suoi effetti.
L’interesse degli autori è soprattutto di tipo ecologico-conservazionistico, un campo di indagine in cui i dati temporali sono molto difficili da recuperare (si parla di dinamiche che si svolgono in decenni), mentre i dati spaziali sono molto affidabili e a basso costo grazie ai sistemi di rilevamento satellitare. Si immagini allora una perturbazione di un ecosistema (gli autori fanno l’esempio del recente incendio che ha mandato in fumo una parte considerevole delle foreste dell’Australia occidentale): l’estensione di zone ‘di influenza’ dell’evento a grande distanza dal confine fisico del fuoco sarebbe un segno di ‘stato critico’, reso evidente dalla catastrofe in quanto ci parla di una struttura di forte correlazione tra zone, che è sicuro indice di stress.
Ciò a cui gli autori non prestano attenzione (ma non era questo il tema dell’articolo) è il fatto che i loro dati sperimentali implicano l’esistenza di una ‘memoria’ della situazione precedente alla perturbazione, la cui natura è di difficile interpretazione ma che si presenta come un fenomeno biologico del tutto inaspettato.
La figura successiva riporta l’andamento della volatilità (espressa come coefficiente di variazione tra diverse repliche del sistema) in funzione del fattore di diluizione all’avvicinarsi del punto critico per lo schema a coltura isolata (linea rossa) e a colture connesse (linea blu).
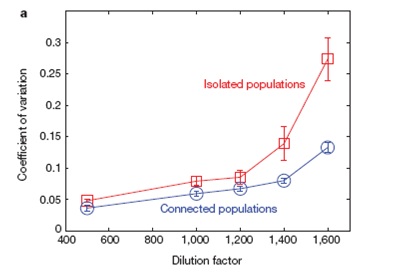
Come dicevamo prima si nota evidente la separazione tra i due schemi sperimentali all’approssimarsi del valore 1700 che abbiamo indicato essere il punto di crisi nel fattore di diluizione: il sistema isolato mostra ‘segnali di crisi’ virtualmente assenti nel sistema ‘misto’ o a popolazioni connesse. Cosa sta alla base di queste differenze non possiamo saperlo, ma di sicuro possiamo dire che, a parità di condizioni di diluizione, le colonie provenienti dalla stessa origine ‘sentono meglio’ che c’è qualcosa che non va rispetto alle altre e, visto che le condizioni di crescita sono identiche, questo può solo avvenire attraverso due possibili meccanismi generali (non necessariamente alternativi):
A) un ricordo delle condizioni iniziali particolari della colonia madre;
B) un linguaggio comune tra le cellule della stessa colonia differenziato da quello di cellule estranee.
Entrambi i meccanismi aprono degli orizzonti sconvolgenti sulla presenza di fenomeni biologici che la nostra scienza è ben lontana dal comprendere e che ci ricordano la necessità di coltivare lo stupore e la meraviglia nell’osservazione della natura, laddove troppo spesso sembriamo occupati a considerare la natura come una pura sorgente di prodotti manipolabili e ad esaltare la nostra tecnologia che rappresenta una prova dell’unicità dell’animo umano e non certo un mezzo per renderci autonomi dalla natura come troppo spesso sembra avvenire.
