Un caro saluto ai miei piccoli lettori. Questa volta vorrei parlarvi di fluidi (e quindi di liquidi e gas) e, in particolare, di cosa succede quando un fluido è in movimento. Tanto per cominciare inizierei dai liquidi che, a differenza dei gas, non sono comprimibili – mantengono, cioè, invariato il proprio volume anche se li si schiaccia – e quindi sono un po’ più facili da trattare. La situazione più semplice è quella in cui il nostro liquido – per esempio acqua – scorre con un moto laminare (cioè senza turbolenze) in un condotto con una sezione circolare che non cambia di dimensioni lungo il suo tragitto ed è disposto orizzontalmente (così non ci complichiamo la vita con gli effetti della gravità…). In questo caso non succede nulla di particolarmente significativo: a regime, infatti, il liquido all’interno del condotto si muove a velocità costante nella direzione in cui viene spinto da qualche marchingegno – per esempio una pompa o un semplice pistone come quello delle siringhe (vedi figura).
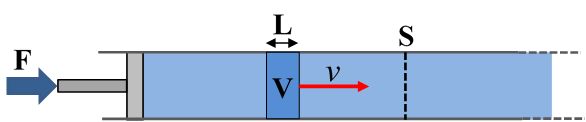
La velocità del liquido nel condotto
Cosa significa che il liquido si muove a velocità costante? Da un punto di vista microscopico la risposta corretta è che tutte le sue molecole si muovono nel tubo alla stessa velocità. Ma questo non è del tutto vero in un caso reale. Le molecole più periferiche – quelle, cioè, che scorrono in prossimità della parete del condotto – infatti, vengono frenate dall’inevitabile attrito con la parete stessa e quindi fluiscono un po’ più lentamente di quelle al centro.
Per semplicità, allora, consideriamo un caso ideale (dove questo problema viene trascurato) e, sempre idealmente, isoliamo all’interno del condotto un certo volume di liquido: per esempio una porzione di liquido di forma cilindrica (V) dello stesso diametro del tubo e con un certo spessore (L), come mostrato in figura.
Possiamo, allora, affermare che il liquido si muove a velocità costante quando questo volume impiega sempre lo stesso tempo a transitare attraverso una qualunque sezione trasversale del tubo – vale a dire attraverso qualunque piano ideale che taglia perpendicolarmente il condotto (indicato con S in figura).
Se, per esempio, il volume considerato è spesso un centimetro e impiega un secondo ad attraversare la sezione trasversale del tubo, allora, possiamo dire che la velocità di scorrimento di questo volume – e quindi, per continuità, anche quella dell’intera colonna liquida presente nel condotto – è di un centimetro al secondo.
Ricordiamo, inoltre, che la quantità di liquido che transita in un secondo attraverso una sezione del condotto (nel nostro esempio è proprio il volume V) viene definita portata e indica la capacità di trasporto del condotto. Più grande è la portata, infatti, maggiore è la quantità di liquido che può essere trasferita attraverso il condotto ogni secondo.
Dunque, ricapitolando, in un tubo orizzontale a sezione costante, quando tutto è a regime, il liquido che scorre al suo interno si muove a velocità costante.
La pressione del liquido nel condotto
Ma cosa possiamo dire a proposito della sua pressione? La pressione, vale a dire forza esercitata su ciascun punto del liquido dal liquido circostante (e che è la stessa in tutte le direzioni, come vi ho già raccontato a proposito della pressione atmosferica), non cambia lungo l’intero percorso del condotto. Essa dipende principalmente dalla forza che fa muovere l’intera colonna liquida: maggiore è questa spinta più grande è la pressione all’interno del condotto.
Un condotto orizzontale con una sezione variabile
Consideriamo ora un caso un po’ più complesso: un condotto orizzontale ma con una sezione variabile, come per esempio quello mostrato in figura, dove la sezione del tubo si restringe passando da S1 a S2.
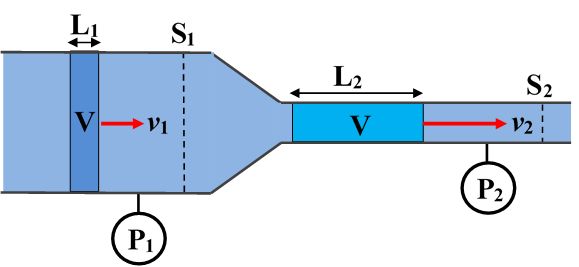
Cosa succede al liquido che fluisce al suo interno? La cosa che salta subito all’occhio è che se consideriamo un certo volume di liquido in transito nella parte più larga del condotto (indicato con V in figura), essendo il liquido incomprimibile, per questioni puramente geometriche a valle del restringimento questo stesso volume deve occupare un tratto di tubo più lungo (come mostrato in figura, il tratto L2 è maggiore del tratto L1). E questo ha conseguenze molto importanti. Siccome in condizioni stazionarie la portata del liquido è costante, vale a dire che in tutti i punti del condotto la quantità di liquido che lo attraversa in un certo intervallo di tempo è sempre la stessa, questo significa che la velocità del liquido deve necessariamente crescere dove la sezione del condotto si restringe. Per capirci meglio: se per esempio attraverso la sezione S1 (vedi figura) in un secondo passano 10 litri d’acqua, anche attraverso la sezione S2, che è più piccola, in un secondo devono transitare sempre 10 litri d’acqua.
Ma, siccome nella parte più stretta del condotto 10 litri d’acqua occupano una lunghezza maggiore, per attraversare la sua sezione in un secondo, l’acqua dovrà per forza scorrere a una velocità maggiore di quella che aveva prima della strozzatura.
In definitiva, quindi, possiamo affermare che in un condotto a sezione variabile la velocità del fluido che lo percorre cresce nei punti dove il condotto si restringe. Cosa, per altro, nota fin dall’antichità. Se vi è capitato di visitare un vecchio mulino ad acqua, infatti, avrete sicuramente notato che il condotto dell’acqua si restringe poco prima che il getto d’acqua colpisca le pale della ruota del mulino; e questo proprio per aumentarne la velocità (e quindi anche la spinta esercitata sulle pale).
Cosa succede alla pressione?
Contrariamente a quanto vorrebbe suggerirci il nostro buon senso, la pressione del liquido ha un comportamento opposto a quello della sua velocità. Sembrerebbe, infatti, abbastanza ragionevole aspettarsi che la pressione del liquido debba aumentare dove il tubo si restringe. E invece no! Anziché aumentare dove il condotto è più stretto, proprio lì la pressione del liquido si riduce. Se misurassimo la pressione dopo il restringimento del condotto (P2 in figura), infatti, scopriremmo che il suo valore è minore di quello misurato prima della strozzatura (P1 in figura).
A livello intuitivo, questa diminuzione può essere giustificata dal fatto che la pressione persa è stata spesa per aumentare la velocità del liquido. In altre parole, la differenza di pressione a valle del restringimento è esattamente quella che serve per dare una spinta e accelerare il liquido nel condotto proprio là dove è più stretto, garantendo in questo modo che la portata rimanga sempre la stessa.
Volendo generalizzare, allora, possiamo affermare che la pressione di un fluido in movimento cambia in funzione della sua velocità, e precisamente: diminuisce dove la sua velocità aumenta e, per converso, aumenta dove la sua velocità diminuisce. Questo fenomeno è noto anche come Effetto Venturi, dal nome del suo scopritore: il sacerdote e fisico Giovanni Battista Venturi (1746 – 1822).
L’effetto Venturi
L’effetto Venturi, è bene sottolinearlo, non si verifica solo all’interno delle tubature percorse da liquidi ma, più in generale, riguarda il comportamento di tutti i fluidi in movimento, e quindi anche i gas come l’aria che respiriamo. Ed è proprio nel settore ingegneristico che si occupa di studiare l’impatto dell’aria sugli oggetti in movimento, che l’effetto Venturi ha trovato importanti applicazioni sia in campo aeronautico sia in quello automobilistico.
Nel settore aeronautico, infatti, l’effetto Venturi ricopre un ruolo fondamentale fra i fenomeni che rendono possibile il volo degli aerei. Si tratta, di fatto, del principale (ma non unico) fenomeno responsabile dell’insorgere della forza aerodinamica (denominata portanza) che spinge un aereo verso l’alto durante la fase di decollo e ne permette poi il sostentamento durante il volo.
Come mostrato nella figura, infatti, le ali degli aerei vengono progettate con un profilo tale per cui i filetti d’aria che scorrono sulla loro parte superiore (chiamata dorso) abbiano una velocità maggiore di quelli che scorrono sulla parte inferiore (chiamata invece ventre). Per questo motivo, a causa dell’effetto Venturi, la pressione dell’aria sopra il dorso delle ali risulta minore di quella esercitata dall’aria sul loro ventre e, di conseguenza, per la differenza di pressione l’aereo riceve una spinta diretta dal basso verso l’alto che lo fa sollevare.
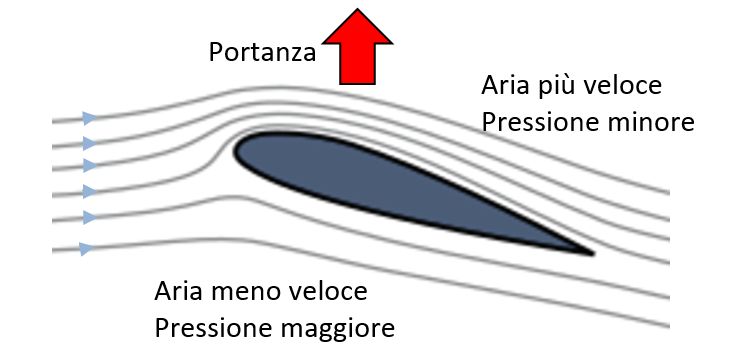
Lo stesso principio, ma applicato in modo opposto, è utilizzato anche nella progettazione delle auto da corsa. In questo caso, infatti, il profilo dell’alettone posteriore dell’auto viene disegnato in modo tale che l’aria che lo investe scorra su di esso più velocemente sulla sua superficie inferiore. Quando questo si verifica, per effetto Venturi la differenza di pressione sull’alettone è tale da generare una spinta diretta verso il basso e così migliorare l’aderenza delle ruote all’asfalto (condizione, questa, fondamentale per poter affrontare le curve ad elevata velocità). La spinta aerodinamica in questo caso prende il nome di deportanza.
Eventi catastrofici
Va tuttavia sottolineato che quando l’effetto Venturi ci sfugge di mano, quando cioè non siamo noi a controllarlo, può anche diventare responsabile di eventi catastrofici. È il caso, per esempio, dello scoperchiamento dei tetti durante gli uragani. Nel corso di un uragano, infatti, i venti sono estremamente violenti – in alcuni casi riescono a raggiungere addirittura velocità superiori ai 250 chilometri orari! – e, di conseguenza, le variazioni di pressione causate dall’effetto Venturi possono avere effetti devastanti.
E questo è proprio quello che succede ai tetti delle abitazioni. Infatti, poiché gli edifici sono abbastanza isolati – e quindi al loro interno la pressione è all’incirca quella atmosferica – le parti esposte ai venti (come il tetto, per l’appunto) risultano sottoposte a una grande differenza di pressione.
Più precisamente, il vento che soffia a forte velocità, per effetto Venturi genera una sensibile diminuzione della pressione esterna proprio in corrispondenza della superficie del tetto, mentre la pressione interna all’abitazione, come dicevamo, non è cambiata in maniera significativa. Il risultato di questa differenza di pressione è una forte spinta dal basso verso l’alto che agisce sul tetto e che, nel peggiore dei casi, non solo è in grado di staccare e fare volar via le tegole che lo ricoprono, ma anche di sollevare e spostare l’intera struttura portante.
Per questo stesso motivo, anche se con conseguenze decisamente meno drammatiche, le tende di un campeggio possono essere divelte e fatte volar via nel corso di un violento acquazzone.
Se avete dormito in tenda durante un campeggio estivo, avrete sicuramente notato che in presenza di un forte vento la tenda si scuote, ma la tendenza principale è quella di gonfiarsi. La cosa non deve stupire. I teli di cui è composta la sua struttura, infatti, vengono in pratica risucchiati verso l’esterno proprio a causa della depressione generata (per effetto Venturi) dal vento che scorre sopra di essi. Ora, se la tenda non è ben fissata al terreno, può accadere che venga addirittura strappata dal suolo e portata via dal vento, lasciando così i suoi sfortunati occupanti esposti alle intemperie!
Un esperimento
Vi propongo ora un semplice esperimento con cui potete verificare voi stessi che l’effetto Venturi esiste per d’avvero. Vi servono solo un foglio di carta formato A4 (quelli che si usano di solito per le stampanti) e del nastro adesivo.
Primo passo.
Piegate il foglio di carta a metà del lato più lungo e appoggiatelo su un tavolo in modo da formare la sagoma di una tenda da campeggio.
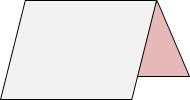
Secondo passo
Fissate il bordo del foglio di carta al tavolo con il nastro adesivo.
Terzo passo
Soffiate all’interno della sagoma di carta. Cosa succede?
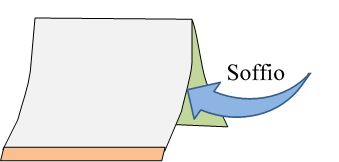
Spiegazione
Mentre soffiate, anziché gonfiarsi, la sagoma di carta viene risucchiata verso l’interno. Il vostro soffio, infatti, fa si che la velocità dell’aria in prossimità della sua superficie interna sia maggiore di quella dell’aria presente al suo esterno (che, invece, è ferma).
Di conseguenza, a causa dell’effetto Venturi, la pressione all’interno della sagoma (dove la velocità dell’aria è maggiore) diventa minore di quella esterna (la pressione atmosferica). Il risultato finale, pertanto, sarà quello di una forza che dall’esterno preme sulla sagoma di carta deformandola. La sagoma, così sollecitata, tenderà perciò a collassare su sé stessa piegandosi verso il suo interno.
Sergio Musazzi
(Ricercatore e divulgatore scientifico)















